题目内容
20.在等差数列{an}中,a2=6,其前n项和为Sn.等比数列{bn}的各项均为正数,b1=1,且b2+S4=33,b3=S2(1)求an与bn;
(2)设数列{cn}的前n项和为Tn,且cn=4bn-a5,求使不等式Tn>S6成立的最小正整数n的值.
分析 (1)设等差数列{an}的公差为d,等比数列{bn}的公比为q>0,由于a2=6,b1=1,且b2+S4=33,b3=S2,可得a1+d=6,q+4a1+$\frac{4×3}{2}d$=33,q2=2a1+d.联立解得即可得出.
(2)cn=4bn-a5=4×3n-1-15.可得数列{cn}的前n项和为Tn=2×3n-2-15n.S6=63.不等式Tn>S6,化为2×3n-2-15n>63,即f(n)=2×3n-15n>63.利用其单调性即可得出.
解答 解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q>0,
∵a2=6,b1=1,且b2+S4=33,b3=S2,
∴a1+d=6,q+4a1+$\frac{4×3}{2}d$=33,q2=2a1+d.
联立解得:q=3,a1=3,d=3.
∴an=3+3(n-1)=3n,bn=3n-1.
(2)cn=4bn-a5=4×3n-1-15.
∴数列{cn}的前n项和为Tn=$4×\frac{{3}^{n}-1}{3-1}$-15n=2×3n-2-15n.
S6=$6×3+\frac{6×5}{2}×3$=63.
不等式Tn>S6,化为2×3n-2-15n>63,即f(n)=2×3n-15n>63.
∵f(n+1)-f(n)=2×3n+1-15(n+1)-2×3n+15n=4×3n-15,
当n≥2时,f(n+1)>f(n),即数列f(n)单调递增,
又f(1)=-9<0,f(2)=-12,f(3)=9,f(4)=102>63,
因此使得f(n)=2×3n-15n>63的n的最小值为4.
使不等式Tn>S6成立的最小正整数n的值是4.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、数列的单调性、不等式的性质,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案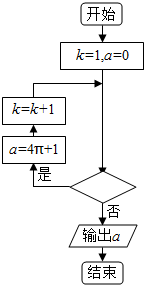
| A. | k<4? | B. | k<5? | C. | k<6? | D. | k<7? |
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
| 测试指标 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
| 零件数 | 2 | 8 | 32 | 38 | 20 |
(2)生产一件零件,若是优质品可盈利40元,若是正品盈利20元,若是次品则亏损20元,若从大量的零件中随机抽取2件,其利润之和记为x(单位:元),求x的分布列及数学期望.