题目内容
已知α,β均为锐角,cos(α+β)=-
,cosα=
,则角cosβ为( )
| 11 |
| 14 |
| 1 |
| 7 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:两角和与差的余弦函数
专题:计算题,三角函数的求值
分析:先利用同角三角函数的基本关系求得sinα和sin(α+β)的值,然后利用cosβ=cosp[(α+β)-α],根据两角和公式求得答案.
解答:
解:α,β均为锐角,
∴sinα=
=
,sin(α+β)=
=
,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=(-
)×
+
×
=
.
故选:D.
∴sinα=
1-
|
4
| ||
| 7 |
1-(
|
5
| ||
| 14 |
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=(-
| 11 |
| 14 |
| 1 |
| 7 |
5
| ||
| 14 |
4
| ||
| 7 |
| 1 |
| 2 |
故选:D.
点评:本题主要考查了两角和公式的化简求值和同角三角函数的基本关系的应用.熟练记忆三角函数的基本公式是解题的基础,属于基础题.

练习册系列答案
相关题目
已知a,b∈R,若a>b,则下列不等式成立的是( )
| A、lga>lgb | ||||||
| B、0.5a>0.5b | ||||||
C、a
| ||||||
D、
|
命题“若x∈N*,则x2≥0”的逆命题,否命题,逆否命题中,正确的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
如果实数x、y满足条件
,则2x+y的最大值为( )
|
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
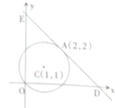 已知圆C的方程为(x-1)2+(y-1)2=2,点A(2,2).
已知圆C的方程为(x-1)2+(y-1)2=2,点A(2,2).