题目内容
已知f(2x+1)=x2-2x,则f(3)= .
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:【方法一】利用换元法求出f(x)的解析式,再计算f(3)的值.
【方法二】根据题意,令2x+1=3,求出x=1,再计算f(3)的值.
【方法二】根据题意,令2x+1=3,求出x=1,再计算f(3)的值.
解答:
解:【方法一】∵f(2x+1)=x2-2x,
设2x+1=t,则x=
,
∴f(t)=(
)2-2×
=
t2-
t+
,
∴f(3)=
×32-
×3+
=-1.
【方法二】∵f(2x+1)=x2-2x,
令2x+1=3,解得x=1,
∴f(3)=12-2×1=-1.
故答案为:-1.
设2x+1=t,则x=
| t-1 |
| 2 |
∴f(t)=(
| t-1 |
| 2 |
| t-1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 5 |
| 4 |
∴f(3)=
| 1 |
| 4 |
| 3 |
| 2 |
| 5 |
| 4 |
【方法二】∵f(2x+1)=x2-2x,
令2x+1=3,解得x=1,
∴f(3)=12-2×1=-1.
故答案为:-1.
点评:本题考查了求函数的解析式以及利用函数的解析式求值的应用问题,是基础题目.

练习册系列答案
相关题目
函数y=2esinx在点x=0处的瞬时变化率为( )
| A、2 | B、-2 | C、2e | D、-2e |
f(x)是定义在D上的函数,若存在区间,使函数f(x)在[m,n]上的值域恰为[km,kn],则称函数f(x)是k型函数.若函数y=-
x2+x[m,n]⊆D是3型函数,则m+n的值为( )
| 1 |
| 2 |
| A、0 | B、8 | C、-4 | D、-4或8 |
已知α,β均为锐角,cos(α+β)=-
,cosα=
,则角cosβ为( )
| 11 |
| 14 |
| 1 |
| 7 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
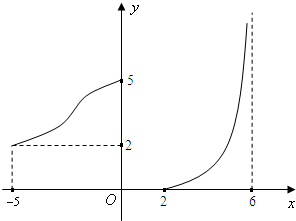 函数y=f(x)的图象如图所示,根据图象回答下列问题:
函数y=f(x)的图象如图所示,根据图象回答下列问题: