题目内容
a,b∈R,则“a=2b”是“复数
为纯虚数”的( )
| a+bi |
| 1-2i |
| A、充分而不必要条件 |
| B、必要不充分条件 |
| C、抽样条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:
=
+
i,进而根据纯虚数的定义,分别判断“a=2b”⇒“复数
为纯虚数”和“a=2b”?“复数
为纯虚数”的真假,进而结合充要条件的定义可得答案.
| a+bi |
| 1-2i |
| a-2b |
| 5 |
| b+2a |
| 5 |
| a+bi |
| 1-2i |
| a+bi |
| 1-2i |
解答:
解:
=
=
+
i,
当“a=2b”时,复数的实部
=0,但虚部
≠0不一定成立,故“a=2b”是“复数
为纯虚数”的不充分条件;
但当“复数
为纯虚数”时,实部
=0,即“a=2b”成立,故“a=2b”是“复数
为纯虚数”的必要条件;
综上所述,“a=2b”是“复数
为纯虚数”的必要不充分条件;
故选:B
| a+bi |
| 1-2i |
| (a+bi)(1+2i) |
| (1-2i)(1+2i) |
| a-2b |
| 5 |
| b+2a |
| 5 |
当“a=2b”时,复数的实部
| a-2b |
| 5 |
| b+2a |
| 5 |
| a+bi |
| 1-2i |
但当“复数
| a+bi |
| 1-2i |
| a-2b |
| 5 |
| a+bi |
| 1-2i |
综上所述,“a=2b”是“复数
| a+bi |
| 1-2i |
故选:B
点评:判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,在复平面内,复数z1,z2对应的向量分别是
,
,则|z1+z2|=( )

| OA |
| OB |

| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
 利用如图所示算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=10内的共有( )个.
利用如图所示算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=10内的共有( )个.| A、2 | B、3 | C、4 | D、5 |
执行如图所示的程序框图,则输出的S为( )


A、-
| ||
| B、2 | ||
C、
| ||
| D、-3 |
执行如图所示的程序框图,输出的S值为( )


| A、126 | B、105 |
| C、91 | D、66 |
函数f(x)=x-sinx是( )
| A、奇函数且单调递增 |
| B、奇函数且单调递减 |
| C、偶函数且单调递增 |
| D、偶函数且单调递减 |
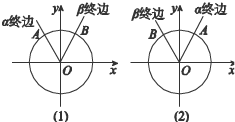 如图,在平面直角坐标系xOy内作单位圆O,以Ox为始边作任意角α,β,它们的终边与单位圆O的交点分别为A,B,
如图,在平面直角坐标系xOy内作单位圆O,以Ox为始边作任意角α,β,它们的终边与单位圆O的交点分别为A,B,