题目内容

6．若回归直线的斜率$\widehatb∈（0，+∞）$，则相关系数r的取值范围为（　　）
A．（0，1]B．[-1，0）C．0D．无法确定

分析 由回归直线的斜率$\widehatb∈（0，+∞）$，是正相关，
得出相关系数r的取值范围是（0，1]．

解答 解：用相关系数r衡量两个变量之间的相关关系的强弱时，
r的绝对值越接近于1，表示两个变量的线性相关性越强，
r的绝对值接近于0时，表示两个变量之间几乎不存在相关关系，
根据相关系数的定义，可知相关系数的取值范围是[-1，1]；
又回归直线的斜率$\widehatb∈（0，+∞）$，是正相关，
此时相关系数r的取值范围是（0，1]．
故选：A．

点评 本题考查了相关系数r的意义以及取值范围问题，是基础题．

练习册系列答案
相关题目
18．已知当x∈[0，1]时，函数y=（mx-1）2 的图象与y=$\sqrt{x}$+m的图象有且只有一个交点，则正实数m的取值范围是（　　）
A．（0，1]∪[2$\sqrt{3}$，+∞）B．（0，1]∪[3，+∞）C．（0，$\sqrt{2}$）∪[2$\sqrt{3}$，+∞）D．（0，$\sqrt{2}$]∪[3，+∞）
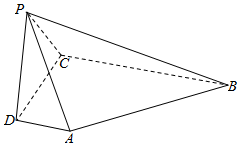19．如图，在四棱锥P-ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．
（Ⅰ）求异面直线AP与BC所成角的余弦值；
（Ⅱ）求证：PD⊥平面PBC；
（Ⅲ）求直线AB与平面PBC所成角的正弦值．
14．已知f（x）是定义在[-1，1]上的奇函数，且f（1）=1，若a，b∈[-1，1]，a+b≠0时，有$\frac{f（a）+f（b）}{a+b}$＞0成立．
（1）判断f（x）在[-1，1]上的单调性，并用定义证明；
（2）解不等式：f（2x-1）＞f（x2-1）；
（3）若f（x）≤m2-3am+1对所有的a∈[-1，1]恒成立，求实数m的取值范围．
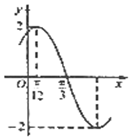1．已知函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的部分图象如图所示，下列说法正确的有（　　）个
①函数f（x）的图象关于直线$x=-\frac{5π}{12}$对称
②函数f（x）在$[-\frac{π}{3}，0]$上单调递增
③函数f（x）的图象关于点$（-\frac{2π}{3}，0）$对称
④将函数y=2sin2x的图象向左平移$\frac{π}{3}$个单位得到f（x）的图象．
A．1B．2C．3D．4
11．已知实数x，y满足不等式组$\left\{\begin{array}{l}{1≤x+y≤2}\\{-1≤x-y≤1}\end{array}\right.$，则z=$\frac{y+1}{x+1}$的最大值是2．
18．求解以下两小题：
（1）91100除以100的余数是几？
（2）若（1+x）6（1-2x）5=a0+a1x+a2x2+…+a11x11．求：
（i）a1+a2+a3+…+a11；
（ii）a0+a2+a4+…+a10．
15．设函数f（x）=x3+3x2+6x+14且f（a）=1，f（b）=19．则a+b=（　　）
A．2B．1C．0D．-2
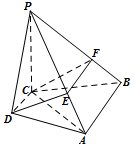16．如图，在四棱锥P-ABCD中，PC⊥平面ABCD，AB∥CD，CD⊥AC，过CD的平面分别与PA，PB交于点E，F．
（1）求证：CD⊥平面PAC；
（2）求证：AB∥EF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网