题目内容
4.已知函数f(x)=ax2-(2a-1)x-lnx(a为常数,a≠0).(Ⅰ)当a<0时,求函数f(x)在区间[1,2]上的最大值;
(Ⅱ)记函数f(x)图象为曲线C,设点A(x1,y1),B(x2,y2)是曲线C上不同的两点,点M为线段AB的中点,过点M作x轴的垂线交曲线C于点N.判断曲线C在点N处的切线是否平行于直线AB?并说明理由.
分析 (Ⅰ)求出函数f(x)的导数,通过讨论a的范围,求出函数f(x)的单调区间,从而求出f(x)的最大值即可;
(Ⅱ)设出M的坐标,分别求出直线AB的斜率k1,C在点N处的切线斜率k2,由k1=k2,得到即$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{1}-{x}_{2}}$=-$\frac{2}{{x}_{1}+{x}_{2}}$,得出矛盾.
解答 解:(Ⅰ)f′(x)=$\frac{(2ax+1)(x-1)}{x}$,
当a<0时,由f′(x)=0,得x1=-$\frac{1}{2a}$,x2=1,又x∈[1,2],则有如下分类:
①当-$\frac{1}{2a}$≥2,即-$\frac{1}{4}$≤a<0时,f(x)在[1,2]上是增函数,
所以f(x)max=f(2)=2-ln2.
②当1<-$\frac{1}{2a}$<2,即-$\frac{1}{2}$<a<-$\frac{1}{4}$时,f(x)在[1,-$\frac{1}{2a}$)上是增函数,在(-$\frac{1}{2a}$,2]上是减函数,
所以f(x)max=f(-$\frac{1}{2a}$)=1-$\frac{1}{4a}$+ln(-2a).
③当-$\frac{1}{2a}$≤1,即a≤-$\frac{1}{2}$时,f(x)在[1,2]上是减函数,
所以f(x)max=f(1)=1-a.
综上,函数f(x)在[1,2]上的最大值为:
f(x)max=$\left\{\begin{array}{l}{2-ln2,-\frac{1}{4}<a≤0}\\{1-\frac{1}{4a}+ln(-2a),-\frac{1}{2}<a<-\frac{1}{4}}\\{1-a,a≤-\frac{1}{2}}\end{array}\right.$;
(Ⅱ)设M(x0,y0),则点N的横坐标为x0=$\frac{{x}_{1}+{x}_{2}}{2}$,
直线AB的斜率k1=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{1}{{x}_{1}-{x}_{2}}$[a(x12-x22)+(1-2a)(x1-x2)+lnx2-lnx1]
=a(x1+x2)+(1-2a)+$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{1}-{x}_{2}}$,
C在点N处的切线斜率
k2=f′(x0)=a(x1+x2)+(1-2a)-$\frac{2}{{x}_{1}+{x}_{2}}$,
假设曲线C在点N处的切线平行于直线AB,则k1=k2,
即$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{1}-{x}_{2}}$=-$\frac{2}{{x}_{1}+{x}_{2}}$,所以ln$\frac{{x}_{2}}{{x}_{1}}$=$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{1+\frac{{x}_{2}}{{x}_{1}}}$,
不妨设x1<x2,ln$\frac{{x}_{2}}{{x}_{1}}$=t>1,则lnt=$\frac{2(t-1)}{1+t}$,
令g(t)=lnt-$\frac{2(t-1)}{1+t}$,(t>1),g′(t)=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
所以g(t)在(1,+∞)上是增函数,又g(1)=0,
所以g(t)>0,即lnt=$\frac{2(t-1)}{1+t}$不成立,
所以曲线C在点N处的切线不平行于直线AB.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及直线的斜率问题,考查分类讨论思想,换元思想,是一道综合题.

| A. | 2 | B. | 1 | C. | 0 | D. | -2 |

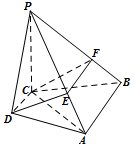 如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥CD,CD⊥AC,过CD的平面分别与PA,PB交于点E,F.
如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥CD,CD⊥AC,过CD的平面分别与PA,PB交于点E,F. 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图. 如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$
如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$