Question

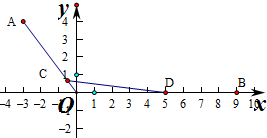
在平面直角坐标系xOy中，已知点A（-3，4），B（9，0），C，D分别为线段OA，OB上的动点，且满足AC=BD
（1）若AC=4，求直线CD的方程；
（2）证明：△OCD的外接圆恒过定点．

Answer 1

考点：圆的一般方程,直线的一般式方程

专题：直线与圆

分析：（1）根据条件确定C，D的坐标，根据直线的两点式方程即可求直线CD的方程；
（2）根据AC=BD，根据待定系数法表示出C，D的坐标，利用圆的一般式方程，即可得到结论．

解答： 解：（1）若AC=4，则BD=4，
∵B（9，0），∴D（5，0），
∵A（-3，4），
∴|OA|=

32+42

=5，则|OC|=1，
直线OA的方程为y=-

4

3

x，
设C（3a，-4a），-1＜a＜0，
则|OC|=

9a2+16a2

=

25a2

=5|a|=-5a=1，
解得a=-

1

5

，
则C（-

3

5

，

4

5

），则CD的方程为

y-0

4 5 -0

=

x-5

- 3 5 -5

，
整理得x+7y-5=0，
即直线CD的方程为x+7y-5=0；
（2）证明：△OCD的外接圆恒过定点．
设C（3a，-4a），-1＜a＜0，
则|AC|=

(3a+3)2+(4+4a)2

=

25(a+1)2

=5|a+1|=5（a+1），
则|BD|=|AC|=5（a+1），则D（4-5a，0），
设△OCD的外接圆的一般方程为x²+y²+Dx+Ey+F=0，
∵O（0，0），C（3a，-4a），-1＜a＜0，D（4-5a，0），
∴圆的方程满足

F=0 9a2+16a2+3aD-4aE+F=0 (4-5a)2+(4-5a)D+F=0

，
即

25a2+3aD-4aE=0 (4-5a)(4-5a+D)=0

，
则

25a+3D-4E=0 D=5a-4

，
解得E=10a-3，F=0，D=5a-4，
则圆的一般方程为x²+y²+（5a-4）x+（10a-3）y=0，
即x²+y²-4x-3y+5a（x+2y）=0，
由

x+2y=0 x2+y2-4x-3y=0

，
解得

x=0 y=0

或

x=2 y=-1

，
即：△OCD的外接圆恒过定点（0，0）和（2，-1）．

点评：本题主要考查直线方程的求解，以及圆的一般式方程的应用，利用待定系数法是解决本题的关键．综合性较强，难度较大．