题目内容
11．
如图所示，正方体ABCD-A1B1C1D1的棱长为2，线段B1D1上有两个动点E，F且EF=$\frac{1}{2}$，则下列结论中正确的有（2）（3）．（1）AC⊥AE；
（2）EF∥平面ABCD；
（3）三棱锥A-BEF的体积为定值：
（4）异面直线AE，BF所成的角为定值．
分析 由线面垂直证得两线垂直判断（1）；
由线面平行的定义证得线面平行判断（2）；
由棱锥的高与底面积都是定值得出体积为定值判断（3）；
由两个极端位置说明两异面直线所成的角不是定值判断（4）．
解答 解：对于（1），由题意及图形知，AC⊥AE，故（1）不正确；
对于（2），由正方体ABCD-A1B1C1D1的两个底面平行，EF在其一面上，故EF与平面ABCD无公共点，故有EF∥平面ABCD，故正确；
对于（3），由几何体的性质及图形知，三角形BEF的面积是定值，A点到面DD1B1B，故可得三棱锥A-BEF的体积为定值，故正确；
对于（4），由图知，当F与B1重合时，与当E与D1重合时，异面直线AE、BF所成的角不相等，故不为定值，故错误．
∴正确命题的序号是（2）（3）．
故答案为（2）（3）．
点评 本题考查棱柱的结构特征，解答本题关键是正确理解正方体的几何性质，且能根据这些几何特征，对其中的点线面和位置关系作出正确判断．熟练掌握线面平行的判断方法，异面直线所成角的定义以及线面垂直的证明是解答本题的关键，是中档题．
练习册系列答案
一线名师提优试卷系列答案
相关题目
6．己知双曲线E的中心在原点，F（5，0）是E的焦点，过F的直线l与E相交于A，B两点，且AB中点为（9，$\frac{9}{2}$），则E的方程为（ ）
| A． | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B． | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 |
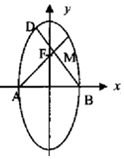已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0），F为椭圆是上焦点，点A，B分别为椭圆的左右顶点，过点B作AF的垂线，垂足为N．
3．在空间直角坐标系中，点P（1，2，-3）关于坐标平面xOy的对称点为（ ）
| A． | （-1，-2，3） | B． | （-1，-2，-3） | C． | （-1，2，-3） | D． | （1，2，3） |
某学校随机抽取部分学生调查其上学路上所需时间（单位：分钟），并将所得数据制成频率分布直方图（如图），若上学路上所需时间的范围为[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．