题目内容
9.已知抛物线y2=4x的焦点为F,过焦点F的直线交抛物线于A、B两点,O为坐标原点,若△AOB的面积为$2\sqrt{6}$,则|AB|=( )| A. | 24 | B. | 8 | C. | 12 | D. | 16 |
分析 设出直线方程,求出A,B两点的纵坐标的差,利用△AOB的面积.求出直线的斜率,然后求解|AB|,
解答 解:抛物线y2=4x焦点为F(1,0),
设过焦点F的直线为:y=k(x-1),
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,可得y2-$\frac{4}{k}$y-4=0,
yA+yB=$\frac{4}{k}$,yAyB=-4,|yA-yB|=$\sqrt{\frac{16}{{k}^{2}}+16}$
△AOB的面积为2$\sqrt{6}$,
可得:$\frac{1}{2}$×1×|yA-yB|=2$\sqrt{6}$,解得k2=$\frac{1}{5}$,
|AB|=$\sqrt{1+\frac{1}{{k}^{2}}}$×|yA-yB|=24.
故选:A.
点评 本题考查抛物线的定义,考查三角形的面积的计算,确定抛物线的弦长是解题的关键.属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.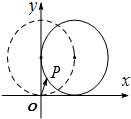 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )
 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )| A. | (1-sin1,1-cos1) | B. | (1+sin1,1-cos1) | C. | (1-sin1,1+cos1) | D. | (1+sin1,1+cos1) |
1.中心角为60°的扇形AOB,它的弧长为2π,则三角形AOB的内切圆半径为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
14.已知a=${∫}_{0}^{1}$(x2-1)dx,b=1-log23,c=cos$\frac{5π}{6}$,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | b<c<a |
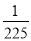 B.
B.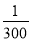 C.
C.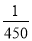 D.以上全不对
D.以上全不对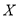 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,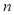 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.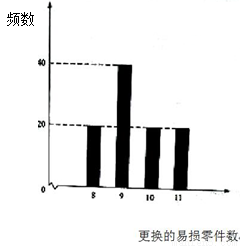
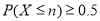 ,确定
,确定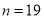 与
与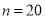 之中选其一,应选用哪个?
之中选其一,应选用哪个?