题目内容
1.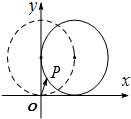 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )| A. | (1-sin1,1-cos1) | B. | (1+sin1,1-cos1) | C. | (1-sin1,1+cos1) | D. | (1+sin1,1+cos1) |
分析 设滚动后的圆的圆心为C并设∠BCP=θ,求出⊙C的方程和参数方程,由题意求出角θ,再由三角函数的诱导公式,化简可得P为(1-sin1,1-cos1),即可求出$\overrightarrow{OP}$的坐标.
解答 解:设滚动后的圆的圆心为C,切点为A(2,0),连接CP,
过C作与x轴正方向平行的射线,交圆C于B(2,1),设∠BCP=θ,
∵⊙C的方程为(x-1)2+(y-1)2=1,
∴根据圆的参数方程,得P的坐标为(1+cosθ,1+sinθ),
∵单位圆的圆心的初始位置在(0,1),圆滚动到圆心位于(1,1)
∴∠ACP=1,可得θ=$\frac{3π}{2}$+1,
可得cosθ=cos($\frac{3π}{2}$-1)=-sin1,sinθ=sin($\frac{3π}{2}$-1)=-cos1,
代入上面所得的式子,得到P的坐标为(1-sin1,1-cos1),
所以$\overrightarrow{OP}$的坐标是(1-sin1,1-cos1),
故选A.
点评 本题根据半径为1的圆的滚动,求一个向量的坐标,考查了圆的参数方程和平面向量的坐标表示的应用等知识点,属于中档题.

练习册系列答案
相关题目
13.两条异面直线所成的角是60°,那么过空间任意一点与a,b都成60°的直线有几条( )
| A. | 1 | B. | 2 | C. | 4 | D. | 3 |
16.在△ABC中,$b=\frac{{4\sqrt{3}}}{3}$,c=2$\sqrt{2}$,C=60°,则A等于( )
| A. | 150° | B. | 75° | C. | 105° | D. | 75°或105° |
9.已知M(4,2)是直线l被椭圆x2+4y2=36所截得的线段AB的中点,则直线l的方程为( )
| A. | 2x+y-8=0 | B. | x+2y-8=0 | C. | x-2y-8=0 | D. | 2x-y-8=0 |
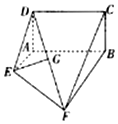 已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.
已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.