题目内容
过点(1,-1)且与直线x+3y-3=0垂直的直线为l,则l被圆x2+y2=4截得的长度为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:由条件利用两条直线垂直的性质,求出l的斜率,可得l的方程,求出弦心距d,再利用弦长公式求出l被圆x2+y2=4截得的长度.
解答:
解:由题意可得,直线l的斜率为3,直线l的方程为y+1=3(x-1),即 3x-y-4=0.
圆心(0,0)到直线l的距离为d=
=
,
故l被圆x2+y2=4截得的长度为2
=2
=
,
故答案为:
.
圆心(0,0)到直线l的距离为d=
| |0-0-4| | ||
|
| 4 | ||
|
故l被圆x2+y2=4截得的长度为2
| r2-d2 |
4-
|
2
| ||
| 5 |
故答案为:
2
| ||
| 5 |
点评:本题主要考查两条直线垂直的性质,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
相关题目
若命题“?x0∈R,2x02-3ax0+9<0”为假命题,则实数a的取值范围是( )
A、[-2
| ||||
B、(-2
| ||||
C、(-∞,-2
| ||||
D、(-∞,-2
|
下列函数中,其图象关于x=
π对称的是( )
| 5 |
| 6 |
A、y=sin(x-
| ||
B、y=sin(x-
| ||
C、y=sin(x+
| ||
D、y=sin(x+
|
(1-
)5的展开式x2的系数是( )
| x |
| A、-5 | B、5 | C、-10 | D、10 |
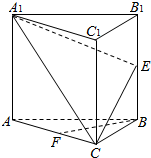 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.