题目内容
已知函数f(x)=αx+
(其中α,b为常数)的图象经过﹙1,2﹚,﹙2,
)两点.
(Ⅰ)求函数f(x)的解析式,并判断f(x)的奇偶性.
(Ⅱ)用定义证明f(x)在区间﹙0,1]上单调递减.
| b |
| x |
| 5 |
| 2 |
(Ⅰ)求函数f(x)的解析式,并判断f(x)的奇偶性.
(Ⅱ)用定义证明f(x)在区间﹙0,1]上单调递减.
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:计算题,证明题,函数的性质及应用
分析:(Ⅰ)f(x)的图象经过两点,把这两点的坐标代入解析式,可求得a、b的值;
(Ⅱ)用定义法证明函数的增减性时,基本步骤是:一取值,二作差,三判正负.四下结论.
(Ⅱ)用定义法证明函数的增减性时,基本步骤是:一取值,二作差,三判正负.四下结论.
解答:
(Ⅰ)解:∵f(x)=ax+
的图象经过(1,2),(2,
)两点;
∴有
,解得
;
∴f(x)的解析式为f(x)=x+
,(其中x≠0),
则定义域关于原点对称,
且f(-x)=-x-
=-(x+
)=-f(x),
则f(x)为奇函数;
(Ⅱ)证明:任取x1,x2,且0<x1<x2≤1,
则f(x1)-f(x2)=(x1+
)-(x2+
)=(x1-x2)+(
-
)=
;
∵0<x1<x2≤1,
∴x1x2<1,x1-x2<0,x1x2-1<0,x1x2>0;
∴f(x1)-f(x2)>0,即f(x1)>f(x2);
∴f(x)在(0,1]上是减函数.
| b |
| x |
| 5 |
| 2 |
∴有
|
|
∴f(x)的解析式为f(x)=x+
| 1 |
| x |
则定义域关于原点对称,
且f(-x)=-x-
| 1 |
| x |
| 1 |
| x |
则f(x)为奇函数;
(Ⅱ)证明:任取x1,x2,且0<x1<x2≤1,
则f(x1)-f(x2)=(x1+
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x1 |
| 1 |
| x2 |
| (x1-x2)(x1x2-1) |
| x1x2 |
∵0<x1<x2≤1,
∴x1x2<1,x1-x2<0,x1x2-1<0,x1x2>0;
∴f(x1)-f(x2)>0,即f(x1)>f(x2);
∴f(x)在(0,1]上是减函数.
点评:本题考查了用待定系数法求函数的解析式以及用定义法证明函数的单调性问题,是基础题.

练习册系列答案
相关题目
函数y=
+ln(x+1)的定义域为( )
| x-1 |
| A、{x|x≥-1} |
| B、{x|x≥1} |
| C、{x|x>1} |
| D、{x|x>-1} |
四棱锥P-ABCD的底面与侧面的形状和大小如图所示.
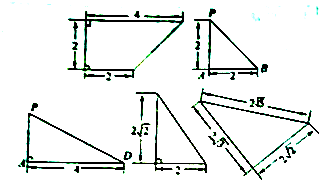
(1)画出该四棱锥的直观图,并证明:当E为PA的中点时,BE∥平面PCD;
(2)若从该四棱锥的8条棱中,任取2条棱,则恰好满足相互垂直的概率是多少?

(1)画出该四棱锥的直观图,并证明:当E为PA的中点时,BE∥平面PCD;
(2)若从该四棱锥的8条棱中,任取2条棱,则恰好满足相互垂直的概率是多少?
设I={2,4,a2-a-3},A={4,1-a},若∁IA={-1},则a=( )
| A、2 | B、-1 | C、0 | D、-1或2 |
已知向量
=(2,-3),
=(x,6),且
∥
,则|
+
|的值为( )
| p |
| q |
| p |
| q |
| p |
| q |
A、
| ||
| B、13 | ||
| C、5 | ||
D、
|