题目内容
已知数列{an}中,a1=
,an=2-
,(n≥2),求an的值.
| 3 |
| 5 |
| 1 |
| an-1 |
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:由a1=
,an=2-
,(n≥2),分别取n=2,3,4,5,6,…,可得:a2=
,a3=-1,a4=3,a5=
,a6=
,…,猜想an=
,验证即可.
| 3 |
| 5 |
| 1 |
| an-1 |
| 1 |
| 3 |
| 5 |
| 3 |
| 7 |
| 5 |
| 2n-5 |
| 2n-7 |
解答:
解:由a1=
,an=2-
,(n≥2),
分别取n=2,3,4,5,6,…,
可得:a2=
,a3=-1,a4=3,a5=
,a6=
,…,
猜想an=
,
验证an+1=2-
=
=
成立.
| 3 |
| 5 |
| 1 |
| an-1 |
分别取n=2,3,4,5,6,…,
可得:a2=
| 1 |
| 3 |
| 5 |
| 3 |
| 7 |
| 5 |
猜想an=
| 2n-5 |
| 2n-7 |
验证an+1=2-
| 1 | ||
|
| 2n-3 |
| 2n-5 |
| 2(n+1)-5 |
| 2(n+1)-7 |
点评:本题考查了通过观察分析猜想归纳求数列的通项公式的方法,考查了分析问题与解决问题的能力,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
已知实数1,m,9成等比数列,则圆锥曲线
+y2=1的离心率为( )
| x2 |
| m |
A、
| ||||||
| B、2 | ||||||
C、
| ||||||
D、
|
四棱锥P-ABCD的底面与侧面的形状和大小如图所示.
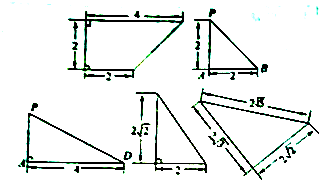
(1)画出该四棱锥的直观图,并证明:当E为PA的中点时,BE∥平面PCD;
(2)若从该四棱锥的8条棱中,任取2条棱,则恰好满足相互垂直的概率是多少?

(1)画出该四棱锥的直观图,并证明:当E为PA的中点时,BE∥平面PCD;
(2)若从该四棱锥的8条棱中,任取2条棱,则恰好满足相互垂直的概率是多少?
已知两条直线m,n,两个平面α,β,下列四个结论中正确的是( )
| A、若m⊥α,α⊥β,n∥β,则m∥n |
| B、若α∥β,m∥α,n∥β,则m∥n |
| C、若m⊥n,m⊥α,n⊥β,则α⊥β |
| D、若m⊥n,m∥α,n∥β,则α⊥β |