题目内容
已知函数f（x）=3ax2+6x-1，（a∈R），若?x∈R，不等式f（x）≤4x恒成立，则实数a的取值范围 ．
考点：函数恒成立问题
专题：函数的性质及应用
分析：先对a进行讨论，当a=0时，不等式为不恒成立．当a≠0时，利用不等式恒成立的条件进行转化，然后求解．
解答：
解：∵f（x）=3ax2+6x-1，（a∈R），若?x∈R，不等式f（x）≤4x恒成立，
∴3ax2+6x-1≤4x，?x∈R，不等式恒成立，
∴3ax2+2x-1≤0，?x∈R，不等式恒成立，
①若a=0，则原不等式等价为2x-1≤0，此时不等式不恒成立，所以a≠0．
②若a≠0，则要使不等式3ax2+2x-1≤0恒成立，
则有
，即
，解得 a≤-
．
综上满足不等式ax2-ax+2＞0在R上恒成立的实数a的取值范围a≤-
．
故答案为：a≤-
．
∴3ax2+6x-1≤4x，?x∈R，不等式恒成立，
∴3ax2+2x-1≤0，?x∈R，不等式恒成立，
①若a=0，则原不等式等价为2x-1≤0，此时不等式不恒成立，所以a≠0．
②若a≠0，则要使不等式3ax2+2x-1≤0恒成立，
则有
|
|
| 1 |
| 3 |
综上满足不等式ax2-ax+2＞0在R上恒成立的实数a的取值范围a≤-
| 1 |
| 3 |
故答案为：a≤-
| 1 |
| 3 |
点评：本题主要考查了不等式恒成立问题．对于在R上一元二次不等式恒成立的问题，要转化为抛物线开口方向和判别式来判断．
练习册系列答案
相关题目
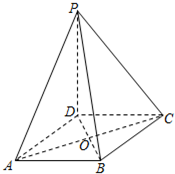如图，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD是菱形