题目内容
已知直线l:2x+y+1=0是三角形的一条内角平分线,且(1,2)和(-1,-1)是三角形的两个顶点,求三角形的第三个顶点的坐标.
考点:两条直线的交点坐标
专题:直线与圆
分析:由对称性可求A(1,2)关于直线2x+y+1=0的对称点A′(m,n),易得直线BC的方程,联立方程组求交点可得.
解答:
解:由题意可设A(1,2),B(-1,-1),
由角平分线可知A(1,2)关于直线2x+y+1=0的对称点A′(m,n)在直线BC上,
则由对称性可知
,
解得
,即A′(-3,0)
∴直线BC的斜率kA′B=
=-
,
∴直线BC的方程为:y-0=-
(x+3),即x+2y+3=0.
再联立
,可解得
,
∴三角形的第三个顶点C的坐标为:(
,-
)
由角平分线可知A(1,2)关于直线2x+y+1=0的对称点A′(m,n)在直线BC上,
则由对称性可知
|
解得
|
∴直线BC的斜率kA′B=
| -1-0 |
| -1-(-3) |
| 1 |
| 2 |
∴直线BC的方程为:y-0=-
| 1 |
| 2 |
再联立
|
|
∴三角形的第三个顶点C的坐标为:(
| 1 |
| 3 |
| 5 |
| 3 |
点评:本题考查两直线交点的坐标,涉及对称性,属基础题.

练习册系列答案
相关题目
设双曲线
-
=1(a>0,b>0)的渐近线方程为y=±
x,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
4名同学要在同一天上、下午到实验室做A,B,C,D,E五个操作实验,每个同学上下午各做一个实验,且不重复,若上午不能做D实验,下午不能做E实验,则不同的安排方式共有( )
| A、144种 | B、192种 |
| C、216种 | D、264种 |
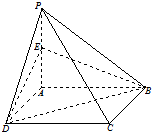 如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E为PA中点.
如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E为PA中点.