题目内容
19．如图，在平行四边形ABCD中，F是BC边的中点，AF交BD于E，若$\overrightarrow{BE}=λ\overrightarrow{ED}$，则λ=$\frac{1}{2}$．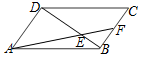
分析 根据平行得到对应边成比例，即可求出λ的值．
解答 解：∵AD∥BC，F是BC边的中点，
∴$\frac{BE}{ED}$=$\frac{BF}{AD}$=$\frac{1}{2}$，
∴$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{ED}$，
∵$\overrightarrow{BE}=λ\overrightarrow{ED}$，
∴λ=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$
点评 本题考查了平行线分线段成比例定理，以及共线向量的问题，属于基础题．
练习册系列答案
相关题目
7．直线ax+by=1（b≥-1）和以A（1，0），B（2，1）为端点的线段相交，则$\frac{b}{a}$取不到的值为（ ）
| A． | -1 | B． | -2 | C． | -$\frac{1}{2}$ | D． | 1 |
14．下列关于函数y=tan（x+$\frac{π}{3}$）的说法正确的是（ ）
| A． | 在区间（-$\frac{π}{6}$，$\frac{5π}{6}$）上单调递增 | B． | 最小正周期是π | ||
| C． | 图象关于点（$\frac{π}{4}$，0）成中心对称 | D． | 图象关于直线x=$\frac{π}{6}$成轴对称 |
4．某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）
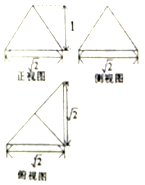
| A． | $\frac{2}{3}$ | B． | 1 | C． | $\frac{1}{3}$ | D． | 2 |
11．已知函数$f（x）=\frac{2}{3}{x^3}+a{x^2}-（a-b）x+c$的两个极值点分别为x1，x2，且x1∈（-∞，-1），x2∈（-1，0），点P（a，b）表示的平面区域为D，若函数y=logm（x+2）（m＞0，m≠1）的图象经过区域D，则实数m的取值范围是（ ）
| A． | （3，+∞） | B． | [3，+∞） | C． | （1，3） | D． | （1，3] |
8．若$f（x）=\left\{{\begin{array}{l}{f（x-5），x＞0}\\{{2^x}+\int_0^{\frac{π}{6}}{cos3tdt，x≤0}}\end{array}}\right.$，则f（2017）=（ ）
| A． | $\frac{1}{24}$ | B． | $\frac{11}{24}$ | C． | $\frac{5}{6}$ | D． | $\frac{1}{2}$ |
如图，在菱形ABCD中，M为AC与BD的交点，∠BAD=$\frac{π}{3}$，AB=3，将△CBD沿BD折起到△C1BD的位置，若点A，B，D，C1都在球O的球面上，且球O的表面积为16π，则直线C1M与平面ABD所成角的正弦值为$\frac{4\sqrt{3}}{7}$．