题目内容
9.已知直线l:y=kx+m(m为常数)和双曲线$\frac{x^2}{9}-\frac{y^2}{4}$=1恒有两个公共点,则斜率k的取值范围为(-$\frac{2}{3}$,$\frac{2}{3}$).分析 法一、由题意画出图形,求出双曲线的渐近线方程,结合对任意实数m,直线l:y=kx+m(m为常数)和双曲线$\frac{x^2}{9}-\frac{y^2}{4}$=1恒有两个公共点即可得到k的取值范围;
法二、联立直线方程和双曲线方程,由二次项系数不为0,且判别式大于0恒成立即可求得k的范围.
解答 解:法一、由双曲线$\frac{x^2}{9}-\frac{y^2}{4}$=1,得a2=9,b2=4,∴a=3,b=2.
∴双曲线的渐近线方程为y=$±\frac{2}{3}x$,
如图,
∵直线l:y=kx+m(m为常数)和双曲线$\frac{x^2}{9}-\frac{y^2}{4}$=1恒有两个公共点,
∴$-\frac{2}{3}$<k<$\frac{2}{3}$.
法二、联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}=1}\end{array}\right.$,得(4-9k2)x2-18kmx-9m2-36=0.
∴$\left\{\begin{array}{l}{4-9{k}^{2}≠0}\\{△=324{k}^{2}{m}^{2}+(16-36{k}^{2})(9{m}^{2}+36)>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{k≠±\frac{2}{3}}\\{3{6}^{2}•{k}^{2}<144{m}^{2}+16×36}\end{array}\right.$,∴$-\frac{2}{3}<k<\frac{2}{3}$.
故答案为:(-$\frac{2}{3}$,$\frac{2}{3}$).
点评 本题考查直线与双曲线的位置关系,考查了数形结合的解题思想方法,是中档题.

| A. | “?x0∈(0,+∞),lnx0≤3-x0 | B. | ?x∈(0,+∞),lnx>3-x | ||
| C. | ?x∈(0,+∞),lnx<3-x | D. | ?x∈(0,+∞),lnx≤3-x |
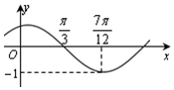 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{4}$个单位,得到函数y=g(x)的图象.
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{4}$个单位,得到函数y=g(x)的图象.