题目内容
9. 如图,在菱形ABCD中,M为AC与BD的交点,∠BAD=$\frac{π}{3}$,AB=3,将△CBD沿BD折起到△C1BD的位置,若点A,B,D,C1都在球O的球面上,且球O的表面积为16π,则直线C1M与平面ABD所成角的正弦值为$\frac{4\sqrt{3}}{7}$.
如图,在菱形ABCD中,M为AC与BD的交点,∠BAD=$\frac{π}{3}$,AB=3,将△CBD沿BD折起到△C1BD的位置,若点A,B,D,C1都在球O的球面上,且球O的表面积为16π,则直线C1M与平面ABD所成角的正弦值为$\frac{4\sqrt{3}}{7}$.
分析 求出球半径为,根据图形找出直线C1M与平面ABD所成角,解三角形即可.
解答 解:如图所示,设O为球心,E、F分别为△ABD、△C1BD的外接圆圆心,
则有OE⊥面ABD,OF⊥面C1BD,
∵菱形ABCD中,∠BAD=$\frac{π}{3}$,AB=3
∴△ABD、△C1BD为等边△,故E、F分别为△ABD、△C1BD的中心.
∵球O的表面积为16π,∴球半径为2.
在直角△AOM中,OA=2,AE=$\frac{2}{3}AM=\sqrt{3}$,⇒QE=1.
tan∠OME=$\frac{OE}{EM}=\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2}{\sqrt{3}}$,
∵C1M⊥DB,AM⊥DB,∴DB⊥面AMC1,
∴∠C1MA(或其补角)就是直线C1M与平面ABD所成角.
∠C1MA=2∠OME,tan∠C1MA=tan(2∠OME)=$\frac{2×\frac{2}{\sqrt{3}}}{1-\frac{4}{3}}=-4\sqrt{3}$,
sin∠C1MA=$\frac{4\sqrt{3}}{7}$,
直线C1M与平面ABD所成角的正弦值为$\frac{4\sqrt{3}}{7}$,
故答案为:$\frac{4\sqrt{3}}{7}$.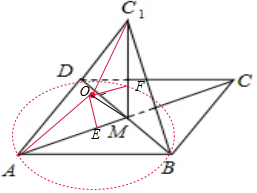
点评 本题考查了棱锥与外接球的关系,找出线面角是解题关键.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知a1,x,y,a2成等差数列,b1,x,y,b2成等比数列.则$\frac{{{{({{a_1}+{a_2}})}^2}}}{{{b_1}{b_2}}}-2$的取值范围是( )
| A. | (0,2] | B. | [-2,0)∪(0,2] | C. | (-∞,-2]∪[2,+∞) | D. | (-∞,-1]∪[1,+∞) |
4.在区间[0,9]上随机取一实数x,则该实数x满足不等式1≤log2x≤2的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{7}{9}$ |
18.设$f(x)=\left\{\begin{array}{l}{2^x},x∈[{0,2}]\\ x+1,x∈[{-2,0})\end{array}\right.$,在集合M={y|y=f(x)}中随机取一个数m,则事件“m>0”的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{5}$ |
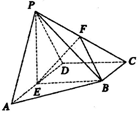 在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.
在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.