题目内容
11.已知函数$f(x)=\frac{2}{3}{x^3}+a{x^2}-(a-b)x+c$的两个极值点分别为x1,x2,且x1∈(-∞,-1),x2∈(-1,0),点P(a,b)表示的平面区域为D,若函数y=logm(x+2)(m>0,m≠1)的图象经过区域D,则实数m的取值范围是( )| A. | (3,+∞) | B. | [3,+∞) | C. | (1,3) | D. | (1,3] |
分析 求出函数的导数,利用函数的极值以及函数的零点列出约束条件,利用线性规划通过目标函数的最优解,求解m的范围.
解答 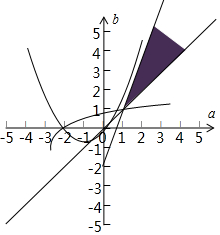 解:由f'(x)=2x2+2ax-(a-b),故f'(x)=0的两根分别为x1,x2,
解:由f'(x)=2x2+2ax-(a-b),故f'(x)=0的两根分别为x1,x2,
由二次方程根的分布得$\left\{\begin{array}{l}4{a^2}+8(a-b)>0\\ f'(-1)<0,\;\\ f'(0)>0\end{array}\right.$,
即$\left\{\begin{array}{l}b<\frac{a^2}{2}+a\\ 3a-b-2>0\\ a-b<0\end{array}\right.$画出该不等式组所表示的平面区域D,
当函数y=logm(x+2)的图象经过点(1,1)时,m=3,
因此当1<m<3时函数图象经过区域D,
故选:C.
点评 本题考查函数的导数的应用,函数的极值以及线性规划的应用,考查转化思想以及计算能力.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
2.数列{an}中,${a_1}+{a_2}+{a_3}+…+{a_n}={3^n}-1$,则${a_1}^2+{a_2}^2+{a_3}^2+…+{a_n}^2$等于( )
| A. | 9n-1 | B. | (3n-1)2 | C. | $\frac{1}{2}({{9^n}-1})$ | D. | $\frac{3}{4}({{3^n}-1})$ |
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}2x+y≥3\\ y≤x\\ 2x-y≤8\end{array}\right.$,则目标函数z=3x-y的最大值为( )
| A. | 2 | B. | 11 | C. | 16 | D. | 18 |
16.已知集合A={-1,0,1,2,3,4},B={x|x2<16,x∈N},则A∩B等于( )
| A. | {-1,0,1,2,3} | B. | {0,1,2,3,4} | C. | {1,2,3} | D. | {0,1,2,3} |
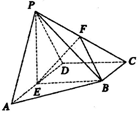 在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.
在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.