题目内容
14.下列关于函数y=tan(x+$\frac{π}{3}$)的说法正确的是( )| A. | 在区间(-$\frac{π}{6}$,$\frac{5π}{6}$)上单调递增 | B. | 最小正周期是π | ||
| C. | 图象关于点($\frac{π}{4}$,0)成中心对称 | D. | 图象关于直线x=$\frac{π}{6}$成轴对称 |
分析 根据正切函数的图象和性质,对选项判断正误即可.
解答 解:对于A,由kπ-$\frac{π}{2}$<x+$\frac{π}{3}$<kπ+$\frac{π}{2}$,k∈Z,
即kπ-$\frac{5π}{6}$<x<kπ+$\frac{π}{6}$,k∈Z,
当k=0时,函数的单调递增区间为(-$\frac{5π}{6}$,$\frac{π}{6}$),
当k=1时,函数的单调递增区间为($\frac{π}{6}$,$\frac{7π}{6}$),
故f(x)在区间(-$\frac{π}{6}$,$\frac{5π}{6}$)上单调递增错误,A错误;
对于B,函数f(x)的最小正周期为T=π,命题正确;
对于C,由x+$\frac{π}{3}$=$\frac{kπ}{2}$,得x=-$\frac{π}{3}$+$\frac{kπ}{2}$,k∈Z,
即函数f(x)的对称中心为(-$\frac{π}{3}$+$\frac{kπ}{2}$,0),
当k=1时,对称中心为($\frac{π}{6}$,0),f(x)图象不关于点($\frac{π}{4}$,0)成中心对称,C错误;
对于D,正切函数是奇函数,图象没有对称轴,D错误.
故选:B.
点评 本题主要考查了与正切函数有关的命题真假的判断问题,熟记正切函数的图象和性质是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
5.在△ABC中,A=135°,C=30°,c=20,则边a的长为( )
| A. | 10$\sqrt{2}$ | B. | 20$\sqrt{2}$ | C. | 20$\sqrt{6}$ | D. | $\frac{20\sqrt{6}}{3}$ |
2.数列{an}中,${a_1}+{a_2}+{a_3}+…+{a_n}={3^n}-1$,则${a_1}^2+{a_2}^2+{a_3}^2+…+{a_n}^2$等于( )
| A. | 9n-1 | B. | (3n-1)2 | C. | $\frac{1}{2}({{9^n}-1})$ | D. | $\frac{3}{4}({{3^n}-1})$ |
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}2x+y≥3\\ y≤x\\ 2x-y≤8\end{array}\right.$,则目标函数z=3x-y的最大值为( )
| A. | 2 | B. | 11 | C. | 16 | D. | 18 |
4.在区间[0,9]上随机取一实数x,则该实数x满足不等式1≤log2x≤2的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{7}{9}$ |
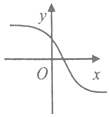
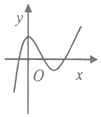
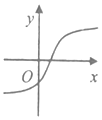
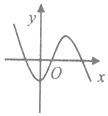
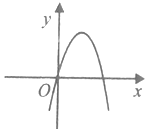 已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )
已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )