题目内容
在(0,2π)内,使sinx-cosx<0成立的x取值范围是( )
A、(
| ||||
B、(0,
| ||||
C、(
| ||||
D、(0,
|
考点:三角函数线
专题:计算题,三角函数的图像与性质
分析:化简得
sin(x-
)<0,结合正弦函数的图象解关于x的不等式得到-
+2kπ<x<
+2kπ,分别取k=0和k=1,并将得到的范围与(0,2π)取交集,可得答案.
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
解答:
解:sinx-cosx<0化简得
sin(x-
)<0
令-π+2kπ<x-
<2kπ(k∈Z),得-
+2kπ<x<
+2kπ
取k=0,得-
<x<
;取k=1,得
<x<
再将以上范围与(0,2π)取交集,可得x∈(0,
)∪(
,2π)
故选:D.
| 2 |
| π |
| 4 |
令-π+2kπ<x-
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
取k=0,得-
| 3π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| 9π |
| 4 |
再将以上范围与(0,2π)取交集,可得x∈(0,
| π |
| 4 |
| 5π |
| 4 |
故选:D.
点评:本题求(0,2π)内使sinx<cosx成立的x取值范围,着重考查了三角函数式的化简和正弦函数的图象与性质等知识,属于基本知识的考查.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
从装有3个红球、2个白球的袋中任取3个球,所取的3个球中至少有1个白球的取法种数是( )
| A、10 | B、3 | C、6 | D、9 |
如图是一个几何体的三视图,则该几何体的体积为( )


| A、27 | ||
B、9
| ||
| C、9 | ||
| D、3 |
一个半径为1的球体经过切割后,剩下部分几何体的三视图如图所示,则剩下部分几何体的体积为( )

A、
| ||
B、
| ||
| C、π | ||
D、
|
执行如图所示的程序,则输出结果S的值为( )


| A、6 | B、14 | C、10 | D、30 |

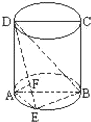 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.