题目内容
高新开发区某公司生产一种品牌笔记本电脑的投入成本是4500元/台,当笔记本电脑销售价为6000元/台时,月销售量为a台;市场分析的结果表明,如果笔记本电脑的销售价提高的百分率为x(0<x<1),那么月销售量减少的百分率为x2.问这种笔记本电脑的售价为多少时,电脑企业的月利润最大?
考点:函数模型的选择与应用
专题:应用题,导数的概念及应用
分析:根据题意,算出每个电脑的利润,计算出销售量,两者相乘即可得到月利润y(元)与x的函数关系式,研究函数的单调性,求函数取最值时x 的取值即可,
解答:
解:依题意,销售价提高后为6000(1+x)元/台,月销售量为a(1-x2)台
则y=a(1-x2)[6000(1+x)-4500],
即y=1500a(-4x3-x2+4x+1)(0<x<1).
(2)y′=1500a(-12x2-2x+4)
令y′=0,得6x2+x-2=0,解得x=
或-
(舍去).
当0<x<
时,y′>0;当
<x<1时,y′<0.
所以,当x=
时,y取得最大值,此时销售价为9000元.
答:笔记本电脑的销售价为9000元时,电脑企业的月利润最大.
则y=a(1-x2)[6000(1+x)-4500],
即y=1500a(-4x3-x2+4x+1)(0<x<1).
(2)y′=1500a(-12x2-2x+4)
令y′=0,得6x2+x-2=0,解得x=
| 1 |
| 2 |
| 2 |
| 3 |
当0<x<
| 1 |
| 2 |
| 1 |
| 2 |
所以,当x=
| 1 |
| 2 |
答:笔记本电脑的销售价为9000元时,电脑企业的月利润最大.
点评:本题考查函数模型的选择与应用,根据实际问题选择合适的模型是解决实际问题的变化关系常用的方法,其步骤是,建立函数模型,求解函数,得出结论,再反馈回实际问题中去.

练习册系列答案
相关题目
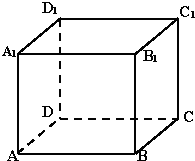 在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是A1B和AC的中点.
在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是A1B和AC的中点.
