题目内容
4.实数x,y满足$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{0≤y≤1}\end{array}\right.$,则z=$\frac{y}{x-2}$的最小值为( )| A. | -$\frac{1}{4}$ | B. | 1 | C. | -1 | D. | 0 |
分析 作出不等式组对应的平面区域,利用直线斜率的几何意义进行求解即可.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
z=$\frac{y}{x-2}$的几何意义是区域内的点到定点C(2,0)的斜率
由图象知CA的斜率最小,
此时最小值为-1,
故选:C.
点评 本题主要考查线性规划的应用,利用数形结合以及直线斜率的几何意义是解决本题的关键.

练习册系列答案
相关题目
9.某城区按以下规定收取水费:若每月用水不超过20m3,则每立方米水费按2元收取;若超过20m3,则超过的部分按每立方米3元收取,如果某户居民在某月所交水费的平均价为每立方米2.20元,则这户居民这月共用水( )
| A. | 46m3 | B. | 44m3 | C. | 26m3 | D. | 25m3 |
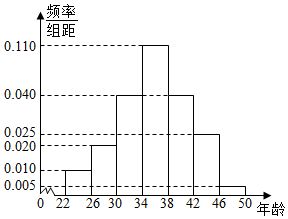 2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地(已婚男性约15000人)随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下;
2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地(已婚男性约15000人)随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下; 如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,E是PC的中点,∠DAC=∠AOB.
如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,E是PC的中点,∠DAC=∠AOB.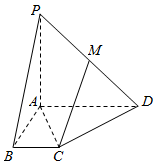 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥BC,BC∥AD,AB=BC=1,AD=2,M为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥BC,BC∥AD,AB=BC=1,AD=2,M为PD的中点.