题目内容
17．已知椭圆的焦点是F1（-2，0），F2（2，0），点P为椭圆上一点，且|PF2|，|F1F2|，|PF1|成等差数列，求此椭圆的标准方程．分析 由已知条件利用椭圆定义和等差数列性质列出方程组，求出a，b，由此能求出椭圆的标准方程．
解答 解：∵椭圆的焦点是F1（-2，0），F2（2，0），点P为椭圆上一点，且|PF2|，|F1F2|，|PF1|成等差数列，
∴$\left\{\begin{array}{l}{c=2}\\{2a=|P{F}_{1}|+|P{F}_{2}|=2|{F}_{1}{F}_{2}|=8}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$，
解得a=4，c=2，b2=16-4=12，
∴此椭圆的标准方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1．
点评 本题考查椭圆的标准方程的求法，是基础题，解题时要认真审题，注意椭圆的性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
7．已知集合A={0，1，2}，B={m，3，4}，若A∩B={2}，则实数m=（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
8．设平面向量$\overrightarrow{OA}$、$\overrightarrow{OB}$满足|$\overrightarrow{OA}$|=2、|$\overrightarrow{OB}$|=1，$\overrightarrow{OA}•\overrightarrow{OB}$=0，点P满足$\overrightarrow{OP}=\frac{m}{{\sqrt{2{m^2}+2{n^2}}}}\overrightarrow{OA}+\frac{{\sqrt{2}n}}{{\sqrt{{m^2}+{n^2}}}}\overrightarrow{OB}$，其中m≥0，n≥0，则点P所表示的轨迹长度为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{π}{2}$ | D． | $\frac{{\sqrt{2}π}}{2}$ |
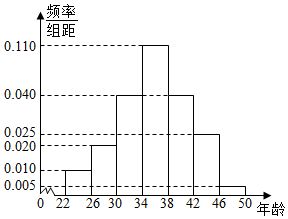2016年1月1日，我国实施“全面二孩”政策，中国社会科学院在某地（已婚男性约15000人）随机抽取了150名已婚男性，其中愿意生育二孩的有100名，经统计，该100名男性的年龄情况对应的频率分布直方图如下；