题目内容

数列{an}的首项为3，{bn}为等差数列且bn=an+1-an（n∈N*）．若则b3=-2，b10=12，则a3=（　　）
A、-3B、3C、8D、-7
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：先利用等差数列的通项公式分别表示出b3和b10，联立方程求得b1和d，进而利用叠加法求得b1+b2+…+bn=an+1-a1，最后利用等差数列的求和公式求得答案．
解答： 解：依题意可知
b1+2d=-2
b1+9d=12
，
求得b1=-6，d=2
∵bn=an+1-an，
∴b1+b2+…+bn=an+1-a1，
∴a3=b1+b2+3=-6-4+3=-7
故选：D．
点评：本题主要考查了数列的递推式．考查了考生对数列基础知识的熟练掌握．
练习册系列答案
相关题目
已知tanθ=
1
3
，则cos2θ+
1
2
sin2θ=
 
．
复数Z=（-1-2i）i的虚部为
 
．
由曲线y=
1
x
，直线y=-x+
5
2
所围成的封闭图形的面积为
 
．
如果复数z（2-3i）=6+4i，则z的模为
 
．
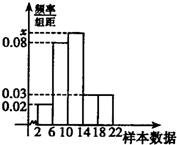为了调查学生每天零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观．样本容量1000的频率分布直方图如图所示，则样本数据落在[6，14）内的频数为（　　）
A、780B、660
C、680D、460
设集合A={1，2，3，4}，B⊆A，已知1∈B，且B中含有3个元素，则集合B有（　　）
A、
A
2
4
个
B、
C
2
3
个
C、
A
2
3
个
D、
C
2
4
个
已知实数x，y满足不等式组
x+3y-3≤0
x-y-3≤0
x≥0
，则2x-y的取值范围是（　　）
A、[-1，3]
B、[-3，-1]
C、[-1，6]
D、[-6，1]
若0＜y＜x＜
π
2
，且tan2x=3tan（x-y），则x+y的可能取值是（　　）
A、
π
6
B、
π
5
C、
π
4
D、
π
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网