题目内容
12.在平面直角坐标系中,已知点B(1,1),曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$(θ为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,点A的极坐标为(4$\sqrt{2}$,$\frac{π}{4}$),直线l的极坐标方程为ρcos(θ-$\frac{π}{4}$)=a,且l过点A,过点B与直线l平行的直线为l1,l1与曲线C相交于两点M,N(Ⅰ)求曲线C上的点到直线l距离的最小值
(Ⅱ)求|MN|的值.
分析 (I)点A的极坐标为(4$\sqrt{2}$,$\frac{π}{4}$),直线l的极坐标方程为ρcos(θ-$\frac{π}{4}$)=a,代入可得a=4$\sqrt{2}$.直线l的极坐标方程为ρcos(θ-$\frac{π}{4}$)=4$\sqrt{2}$,展开为:$\frac{\sqrt{2}}{2}$ρ(cosθ+sinθ)=4$\sqrt{2}$,即可化为直角坐标方程.利用点到直线的距离公式与和差公式、三角函数的单调性即可得出.
(II)设l1的方程为:x+y+m=0,把B(1,1)代入上述方程可得直线l1的方程为:x+y-2=0.可得参数方程:$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),代入曲线C的普通方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.利用根与系数的关系及其|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$即可得出.
解答 解:(I)点A的极坐标为(4$\sqrt{2}$,$\frac{π}{4}$),直线l的极坐标方程为ρcos(θ-$\frac{π}{4}$)=a,∴a=$4\sqrt{2}cos(\frac{π}{4}-\frac{π}{4})$=4$\sqrt{2}$.
∴直线l的极坐标方程为ρcos(θ-$\frac{π}{4}$)=4$\sqrt{2}$,展开为:$\frac{\sqrt{2}}{2}$ρ(cosθ+sinθ)=4$\sqrt{2}$,化为直角坐标方程:x+y-8=0.
∴曲线C上的点到直线l距离d=$\frac{|2cosθ+\sqrt{3}sinθ-8|}{\sqrt{2}}$=$\frac{|\sqrt{7}sin(θ+φ)-8|}{\sqrt{2}}$≥$\frac{8-\sqrt{7}}{\sqrt{2}}$=$\frac{8\sqrt{2}-\sqrt{14}}{2}$,当sin(θ+φ)=1时取等号.
(II)设l1的方程为:x+y+m=0,把B(1,1)代入上述方程可得:m=-2.
∴直线l1的方程为:x+y-2=0.可得参数方程:$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),代入曲线C的普通方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
化为:7t2+2$\sqrt{2}$t-10=0,∴t1+t2=-$\frac{2\sqrt{2}}{7}$,t1•t2=-$\frac{10}{7}$,
∴|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{(-\frac{2\sqrt{2}}{7})^{2}-4×(-\frac{10}{7})}$=$\frac{12\sqrt{2}}{7}$.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程的应用、弦长公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案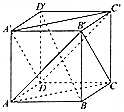
| A. | 平面ACB′∥平面A′C′D | B. | B′C⊥BD′ | ||
| C. | B′C⊥DC′ | D. | BD′⊥平面A′C′D |
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
 我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.
我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.