题目内容
已知f(x)=ax+b(a,b为常数)为指数函数,且图象经过点(2,9),求函数f(x)的解析式.
考点:幂函数的概念、解析式、定义域、值域
专题:函数的性质及应用
分析:根据指数函数的定义,可以得到b=0,再根据图象经过点(2,9),列出关于a的方程,求出a的值,即可得到f(x)的解析式.
解答:
解:∵f(x)=ax+b(a,b为常数)为指数函数,
∴b=0,a>0且a≠1,
∴f(x)=ax,
∵图象经过点(2,9),
∴a2=9,
∴a=±3,
又∵a>0且a≠1,
∴a=3,
∴f(x)的解析式为f(x)=3x.
∴b=0,a>0且a≠1,
∴f(x)=ax,
∵图象经过点(2,9),
∴a2=9,
∴a=±3,
又∵a>0且a≠1,
∴a=3,
∴f(x)的解析式为f(x)=3x.
点评:本题考查了指数函数的概念、解析式.涉及了求函数解析式,求解析式一般选用待定系数法、换元法、配凑法、消元法等.本题选用了待定系数法求解析式,运用待定系数法解题的关键是能正确设出函数的解析式.属于基础题.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
如图是一几何体的三视图,则此几何体的体积是( )
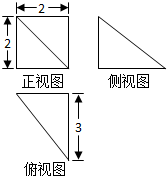

| A、4 | B、8 | C、12 | D、4π |
如果直线x+2y-1=0和kx-y-3=0互相平行,则实数k的值为( )
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|