题目内容
已知数列{an}的前n项和是Sn,且-1,Sn,an+1成等差数列(n∈N*),a1=1.
(1)求数列{an}的通项公式.
(2)若数列{bn}满足b1=a1,bn+1=bn+
(n≥1)求数列{bn}的前n项和Tn.
(3)函数f(x)=log3x,设数列{cn}满足cn=
求数列{cn}的前n项和Rn.
(1)求数列{an}的通项公式.
(2)若数列{bn}满足b1=a1,bn+1=bn+
| 1 |
| 3an |
(3)函数f(x)=log3x,设数列{cn}满足cn=
| 1 |
| (n+3)[f(an)+2] |
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(1)由2Sn=an+1-1,当n≥2时,2Sn-1=an-1,两式相减得
=3,再求得
=3,由此可判断an}是等比数列,可求an;
(2)利用累加法可求bn,再由分组求和可得Tn.
(3)表示出cn,拆项后利用裂项相消法可求得Rn.注意消项规律;
| an+1 |
| an |
| a2 |
| a1 |
(2)利用累加法可求bn,再由分组求和可得Tn.
(3)表示出cn,拆项后利用裂项相消法可求得Rn.注意消项规律;
解答:
解:(1)∵2Sn=an+1-1,当n≥2时,2Sn-1=an-1,
∴2(Sn-Sn-1)=an+1-an,
∴
=3,
∵2a1=a2-1,∴a2=3,
=3,
∴{an}是以1为首项,3为公比的等比数列,
∴an=3n-1.
(2)bn+1=bn+
,∴bn-bn-1=
,
累加得bn=
(1-
),
∴Tn=b1+b2+…+bn=
n-
(1-
).
(3)cn=
=
(
-
),
Rn=
[(
-
)+(
-
)+(
-
)+…+(
-
)]
=
[
-
].
∴2(Sn-Sn-1)=an+1-an,
∴
| an+1 |
| an |
∵2a1=a2-1,∴a2=3,
| a2 |
| a1 |
∴{an}是以1为首项,3为公比的等比数列,
∴an=3n-1.
(2)bn+1=bn+
| 1 |
| 3•3n-1 |
| 1 |
| 3n-1 |
累加得bn=
| 3 |
| 2 |
| 1 |
| 3n |
∴Tn=b1+b2+…+bn=
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 3n |
(3)cn=
| 1 |
| (n+3)(n+1) |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+3 |
Rn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| n+1 |
| 1 |
| n+3 |
=
| 1 |
| 2 |
| 5 |
| 6 |
| 2n+5 |
| (n+2)(n+3) |
点评:该题考查由递推式求数列通项、数列求和、等比数列的性质,裂项相消法对数列求和是高考考查的重点内容,要熟练掌握.

练习册系列答案
相关题目
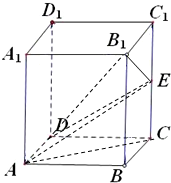 在棱长为2的正方体ABCD-A1B1C1D1中,点E是棱CC1中点
在棱长为2的正方体ABCD-A1B1C1D1中,点E是棱CC1中点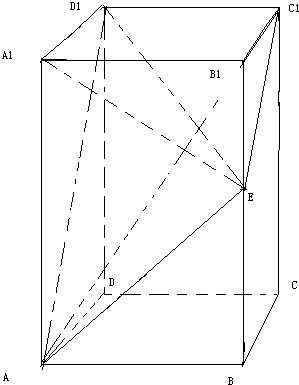 长方体ABCD-A1B1C1D1中,AB=AD=1,BB1=2,E为BB1的中点.(1)求证:AE⊥平面A1D1E;
长方体ABCD-A1B1C1D1中,AB=AD=1,BB1=2,E为BB1的中点.(1)求证:AE⊥平面A1D1E;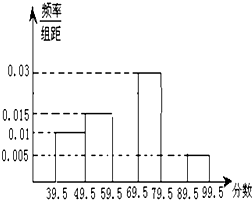 为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题:
为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题: