题目内容
已知△ABC的三内角A,B,C所对的边分别为a,b,c,a=
,b=2,向量
=(-1,
),
=(cosA,sinA),且
•
=1.
(1)求角A;
(2)求
的值.
| 15 |
| m |
| 3 |
| n |
| m |
| n |
(1)求角A;
(2)求
| 1+sin2B |
| cos2B-sin2B |
考点:平面向量的综合题
专题:计算题,三角函数的求值,平面向量及应用
分析:(1)利用向量垂直的充要条件即可得出;
(Ⅱ)利用正弦定理,求出tanB=
,将
化简为
,即可得出结论.
(Ⅱ)利用正弦定理,求出tanB=
| 1 |
| 2 |
| 1+sin2B |
| cos2B-sin2B |
| tanB+1 |
| 1-tanB |
解答:
解:(1)∵向量
=(-1,
),
=(cosA,sinA),且
•
=1,
∴
sinA-cosA=1,
∴sin(A-
)=
,
∵A-
∈(-
,
)
∴A-
=
,
∴A=
;
(2)∵a=
,b=2,
∴sinB=
=
,
∵b<a,
∴tanB=
.
∴
=
=
=
=3.
| m |
| 3 |
| n |
| m |
| n |
∴
| 3 |
∴sin(A-
| π |
| 6 |
| 1 |
| 2 |
∵A-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴A-
| π |
| 6 |
| π |
| 6 |
∴A=
| π |
| 3 |
(2)∵a=
| 15 |
∴sinB=
| bsinA |
| a |
| 1 | ||
|
∵b<a,
∴tanB=
| 1 |
| 2 |
∴
| 1+sin2B |
| cos2B-sin2B |
| (sinB+cosB)2 |
| cos2B-sin2B |
| sinB+cosB |
| cosB-sinB |
| tanB+1 |
| 1-tanB |
点评:熟练掌握向量垂直的充要条件、正弦定理及二倍角公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
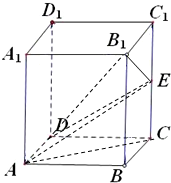 在棱长为2的正方体ABCD-A1B1C1D1中,点E是棱CC1中点
在棱长为2的正方体ABCD-A1B1C1D1中,点E是棱CC1中点