题目内容
18.下列四个说法:①若向量{$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$}是空间的一个基底,则{$\overrightarrow{a}$+$\overrightarrow{b}$、$\overrightarrow{a}$-$\overrightarrow{b}$、$\overrightarrow{c}$}也是空间的一个基底.
②空间的任意两个向量都是共面向量.
③若两条不同直线l,m的方向向量分别是$\overrightarrow{a}$、$\overrightarrow{b}$,则l∥m?$\overrightarrow{a}$∥$\overrightarrow{b}$.
④若两个不同平面α,β的法向量分别是$\overrightarrow{u}$、$\overrightarrow{v}$,且$\overrightarrow{u}$=(1,2,-2)、$\overrightarrow{v}$=(-2,-4,4),则α∥β.
其中正确的说法的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用向量基地的定义、共面与共线向量的定义、空间线面关系即可判断出结论.
解答 解:①若向量{$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$}是空间的一个基底,则{$\overrightarrow{a}$+$\overrightarrow{b}$、$\overrightarrow{a}$-$\overrightarrow{b}$、$\overrightarrow{c}$}也是空间的一个基底,正确.
②空间的任意两个向量都是共面向量,正确.
③若两条不同直线l,m的方向向量分别是$\overrightarrow{a}$、$\overrightarrow{b}$,则l∥m?$\overrightarrow{a}$∥$\overrightarrow{b}$,正确.
④若两个不同平面α,β的法向量分别是$\overrightarrow{u}$、$\overrightarrow{v}$,且$\overrightarrow{u}$=(1,2,-2)、$\overrightarrow{v}$=(-2,-4,4),∵$\overrightarrow{v}$=-2$\overrightarrow{u}$,则α∥β.
其中正确的说法的个数是4.
故选:D.
点评 本题考查了向量基地的定义、共面与共线向量的定义、空间线面关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.设$\overrightarrow{a}$,$\overrightarrow{b}$均为非零向量,则“$\overrightarrow{a}$∥$\overrightarrow{b}$”是“$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同”的( )
| A. | 充要条件 | B. | 充分但不必要条件 | ||
| C. | 必要但不充分条件 | D. | 既不充分也不必要条件 |
13.在区间[1,4]上任取两个实数,则所取两个实数之和大于3的概率为( )
| A. | $\frac{1}{18}$ | B. | $\frac{9}{32}$ | C. | $\frac{23}{32}$ | D. | $\frac{17}{18}$ |
3.函数f(x)的定义域为R,“f(x)是奇函数”是“存在x∈R,f(x)+f(-x)=0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
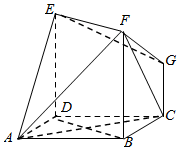 如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.
如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.