题目内容
9.已知抛物线x2=4y焦点为F,直线l与该抛物线相交于点A,B,且$\overrightarrow{OF}$=$\frac{1}{3}$$\overrightarrow{OA}$$+\frac{2}{3}$$\overrightarrow{OB}$,则|$\overrightarrow{AB}$|=$\frac{9}{2}$.分析 可设$\overrightarrow{OC}=\frac{1}{3}\overrightarrow{OA},\overrightarrow{OD}=\frac{2}{3}\overrightarrow{OB}$,且使得四边形OCFD为平行四边形,这样可作出图形,从而有$\overrightarrow{CF}=\overrightarrow{OD}$,可设$A({x}_{1},\frac{{{x}_{1}}^{2}}{4}),B({x}_{2},\frac{{{x}_{2}}^{2}}{4})$,从而可以求出点C的坐标,而F(0,1),从而可以求出$\overrightarrow{CF}$的坐标,且可求出$\overrightarrow{OD}$的坐标,这样即可建立关于x1,x2的方程组,解出x1,x2,从而可得出A,B点的坐标,进而可以求出$|\overrightarrow{AB}|$的值.
解答  解:如图,设$\overrightarrow{OC}=\frac{1}{3}\overrightarrow{OA},\overrightarrow{OD}=\frac{2}{3}\overrightarrow{OB}$,且四边形OCFD为平行四边形;
解:如图,设$\overrightarrow{OC}=\frac{1}{3}\overrightarrow{OA},\overrightarrow{OD}=\frac{2}{3}\overrightarrow{OB}$,且四边形OCFD为平行四边形;
∴$\overrightarrow{CF}=\overrightarrow{OD}$;
设$A({x}_{1},\frac{{{x}_{1}}^{2}}{4}),B({x}_{2},\frac{{{x}_{2}}^{2}}{4})$,则$C(\frac{{x}_{1}}{3},\frac{{{x}_{1}}^{2}}{12})$,$\overrightarrow{OD}=(\frac{2{x}_{2}}{3},\frac{{{x}_{2}}^{2}}{6})$;
∵F(0,1);
∴$\overrightarrow{CF}=(-\frac{{x}_{1}}{3},1-\frac{{{x}_{1}}^{2}}{12})$;
∴$\left\{\begin{array}{l}{-\frac{{x}_{1}}{3}=\frac{2{x}_{2}}{3}}\\{1-\frac{{{x}_{1}}^{2}}{12}=\frac{{{x}_{2}}^{2}}{6}}\end{array}\right.$;
解得$\left\{\begin{array}{l}{{x}_{1}=2\sqrt{2}}\\{{x}_{2}=-\sqrt{2}}\end{array}\right.$,或$\left\{\begin{array}{l}{{x}_{1}=-2\sqrt{2}}\\{{x}_{2}=\sqrt{2}}\end{array}\right.$;
∴A($2\sqrt{2},2$),B($-\sqrt{2},\frac{1}{2}$),或$A(-2\sqrt{2},2),B(\sqrt{2},\frac{1}{2})$;
∴$|\overrightarrow{AB}|=\sqrt{(2\sqrt{2}+\sqrt{2})^{2}+(2-\frac{1}{2})^{2}}=\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 考查向量数乘的几何意义,向量加法的平行四边形法则,抛物线上点的坐标的设法,根据点的坐标求向量的坐标,以及向量坐标的数乘运算,向量相等的概念,根据向量的坐标求向量的长度.

 优生乐园系列答案
优生乐园系列答案| A. | an=2n | B. | an=n2+n+2 | ||
| C. | an=$\left\{\begin{array}{l}{0,n=1}\\{2n-1,n≥2}\end{array}\right.$ | D. | an=$\left\{\begin{array}{l}{0,n=1}\\{2n,n≥2}\end{array}\right.$ |
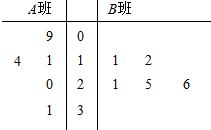 长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).