题目内容
8.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“盖”的术:置如其周,令相承也,又以高乘之,三十六成一,该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈$\frac{1}{36}$L2h,它实际上是将圆锥体积公式中的圆周率π近似取3,那么近似公式V≈$\frac{2}{75}$L2h相当于将圆锥体积公式中的π近似取为$\frac{25}{8}$.分析 用L表示出圆锥的底面半径,得出圆锥的体积关于L和h的式子V=$\frac{{L}^{2}h}{12π}$,令$\frac{{L}^{2}h}{12π}$=$\frac{2{L}^{2}h}{75}$,解出π的近似值.
解答 解:设圆锥的底面半径为r,则圆锥的底面周长L=2πr,
∴r=$\frac{L}{2π}$,
∴V=$\frac{1}{3}π{r}^{2}h$=$\frac{1}{3}π×\frac{{L}^{2}}{4{π}^{2}}×h$=$\frac{{L}^{2}h}{12π}$.
令$\frac{{L}^{2}h}{12π}$=$\frac{2{L}^{2}h}{75}$,得π=$\frac{25}{8}$.
故答案为:$\frac{25}{8}$.
点评 本题考查了圆锥的体积公式,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
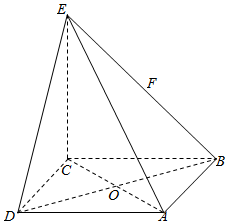 在四棱锥E-ABCD中,底面ABCD是边长为1的正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是边长为1的正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.