题目内容
13.在区间[1,4]上任取两个实数,则所取两个实数之和大于3的概率为( )| A. | $\frac{1}{18}$ | B. | $\frac{9}{32}$ | C. | $\frac{23}{32}$ | D. | $\frac{17}{18}$ |
分析 本题是一个等可能事件的概率,试验发生包含的事件是在区间[0,4]上任取两个数x和y,写出事件对应的集合,做出面积,满足条件的事件是x+y>3,写出对应的集合,做出面积,得到概率.
解答  解:由题意知本题是一个等可能事件的概率,
解:由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是在区间[0,4]上任取两个数x和y,
事件对应的集合是Ω={(x,y)|1≤x≤4,1≤y≤4}
对应的面积是sΩ=9,
满足条件的事件是x+y>3,事件对应的集合是A={(x,y)|1≤x≤4,1≤y≤4,x+y>3}如图
对应的图形(阴影部分)的面积是sA=$9-\frac{1}{2}×1×1$
∴根据等可能事件的概率得到P=1-$\frac{\frac{1}{2}}{9}=\frac{1}{18}$=$\frac{17}{18}$;
故选:D.
点评 本题考查等可能事件的概率,是一个几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到结果,是一个中档题.

练习册系列答案
相关题目
2.已知向量$\overrightarrow{a}$=(cosα,sinβ),$\overrightarrow{b}$=(sinα,cosβ),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则α,β的值可以是( )
| A. | α=$\frac{π}{3}$,β=-$\frac{π}{3}$ | B. | α=$\frac{π}{3}$,β=$\frac{2π}{3}$ | C. | α=$\frac{π}{5}$,β=-$\frac{7π}{10}$ | D. | α=$\frac{π}{3}$,β=-$\frac{π}{6}$ |
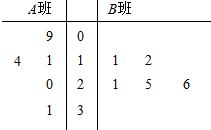 长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).