题目内容
求下列函数的定义域
①y=
②y=
③y=
.
①y=
tanx-
|
②y=
log
|
③y=
| tanx+lg(1-tanx) |
考点:正切函数的单调性,函数的定义域及其求法
专题:函数的性质及应用,三角函数的图像与性质
分析:根据函数的解析式,列出关于自变量的不等式(组),求出解集即可.
解答:
解:①∵y=
,∴tanx-
≥0,
∴tanx≥
,解得x≥
+kπ,且k∈Z;
又x≠
+kπ,k∈Z,
∴函数y的定义域是{x|
+kπ≤x<
+kπ,k∈Z};
②∵y=
,∴log
tanx≥0,
∴0<tanx≤1,解得kπ<x≤
+kπ,且k∈Z;
∴函数y的定义域是{x|kπ<x≤
+kπ,k∈Z};
③∵y=
,∴tanx+lg(1-tanx)≥0,
∴
∴0≤tanx<1,
∴kπ≤x<
+kπ,k∈Z;
∴函数y的定义域是{x|kπ≤x<
+kπ,k∈Z}.
tanx-
|
| 3 |
∴tanx≥
| 3 |
| π |
| 3 |
又x≠
| π |
| 2 |
∴函数y的定义域是{x|
| π |
| 3 |
| π |
| 2 |
②∵y=
log
|
| 1 |
| 2 |
∴0<tanx≤1,解得kπ<x≤
| π |
| 4 |
∴函数y的定义域是{x|kπ<x≤
| π |
| 4 |
③∵y=
| tanx+lg(1-tanx) |
∴
|
∴0≤tanx<1,
∴kπ≤x<
| π |
| 4 |
∴函数y的定义域是{x|kπ≤x<
| π |
| 4 |
点评:本题考查了求函数定义域的应用问题,也考查了三角函数的应用问题,是综合题目.

练习册系列答案
相关题目
已知点A、B、C、D均在球O上,AB=BC=
,AC=3,若三棱锥D-ABC体积的最大值为
,则球O的表面积为( )
| 3 |
3
| ||
| 4 |
| A、36π | ||
| B、16π | ||
| C、12π | ||
D、
|
已知P是△ABC所在平面内一点,若
=
-
,则△PBC与△ABC的面积的比为( )
| AP |
| 3 |
| 4 |
| BC |
| 2 |
| 3 |
| BA |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知非零向量
,
,则“|
-
|=|
|+|
|”是“
+2
=
”成立的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 0 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知a=(log54)2,b=log53,c=ln
,下列结论正确的是( )
| 3 |
| A、a>c>b |
| B、a>b>c |
| C、c>a>b |
| D、b>a>c |
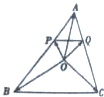 如图,O是△ABC内一点,PQ∥BC,且
如图,O是△ABC内一点,PQ∥BC,且