题目内容
19.(Ⅰ)计算:cos(-$\frac{19π}{6}$);(Ⅱ)已知x∈[$\frac{π}{2}$,$\frac{3π}{2}$],且sinx=-$\frac{3}{5}$,求tanx的值.
分析 (I)利用诱导公式即可得出.
(II)利用同角三角函数基本关系式即可得出.
解答 解:(Ⅰ)cos(-$\frac{19π}{6}$)=$cos(2π+\frac{7π}{6})$=$-cos\frac{π}{6}$=-$\frac{\sqrt{3}}{2}$.
(Ⅱ)∵x∈[$\frac{π}{2}$,$\frac{3π}{2}$],且sinx=-$\frac{3}{5}$,
∴$x∈[π,\frac{3π}{2}]$,∴cosx=$-\sqrt{1-si{n}^{2}x}$=-$\frac{4}{5}$.
∴tanx=$\frac{sinx}{cosx}$=$\frac{3}{4}$.
点评 本题考查诱导公式、同角三角函数的基本关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.设复数z1=1+2i,z2=2-i,i为虚数单位,则z1z2=( )
| A. | 4+3i | B. | 4-3i | C. | -3i | D. | 3i |
7.双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}}{4}$ |
14.已知扇形的半径为3,圆心角为$\frac{2π}{3}$,则扇形的弧长为( )
| A. | 3π | B. | 2π | C. | 360 | D. | 540 |
4.设数列{an}满足:a1=2,an+1=1-$\frac{1}{{a}_{n}}$,记数列{an}的前n项之积为T,则T2017的值为( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | 2 | D. | -2 |
11.某几何体的三视图如图所示,则该几何体的体积为( )
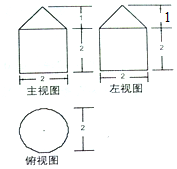

| A. | 2π | B. | $\frac{7}{3}$π | C. | $\frac{8}{3}$π | D. | 4π |
5.已知函数f(x)=ax3+bx(a,b∈R)的图象如图所示,则a,b的关系是( )


| A. | 3a-b=0 | B. | 3a+b=0 | C. | a-3b=0 | D. | a+3b=0 |