题目内容

9．若x，y满足约束条件$\left\{\begin{array}{l}x+y-1≥0\\ y≥2x-2\\ y≤2\end{array}\right.$，且z=kx+y取最小值时的最优解有无数个，则k=-2或1．

分析 先根据约束条件画出可行域，由z=kx+y，利用z的几何意义求最值，要使得取得最小值的最优解有无数个，只需直线z=kx+y与可行域的边界AC，BC平行时，从而得到k值即可．

解答 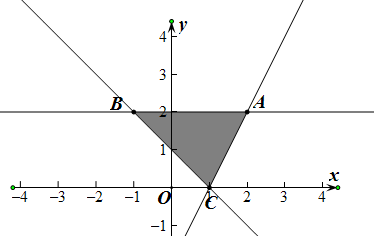解：∵z=kx+y则y=-kx+z，z为直线y=-x+在y轴上的截距，
要使目标函数取得最小值的最优解有无穷多个，
则截距最小时的最优解有无数个．
把z=kx+y平移，使之与可行域中的边界AC，或BC重合即可，
∵A（2，2），B（-1，2），C（1，0），
∴-k=$\frac{2-0}{2-1}$=2或-k=$\frac{2-0}{-1-1}$
解得k=2或k=-1，
故答案为：2或-1．

点评 本题主要考查了简单线性规划的应用、二元一次不等式（组）与平面区域等知识，解题的关键是明确z的几何意义，属于中档题．

练习册系列答案
相关题目
19．B是单位圆O上的点，点A（1，0），点B在第二象限．记∠AOB=θ且sinθ=$\frac{4}{5}$．
（1）求B点坐标；
（2）求$\frac{sin（π+θ）+2sin（\frac{π}{2}-θ）}{2cos（π-θ）}$的值．
20．已知平面向量$\overrightarrow a=（3，2）$，$\overrightarrow b=（-1，2）$，$\overrightarrow c=（4，1）$．
（1）求满足$\overrightarrow a=m\overrightarrow b+n\overrightarrow c$的实数m，n；
（2）若$（{\overrightarrow a+k\overrightarrow c}）⊥（{2\overrightarrow b-\overrightarrow a}）$，求实数k的值．
17．在△ABC中，角A，B，C所对的边分别为a，b，c，若$sinC=\frac{2}{3}，a=3，c=4$，则角A等于（　　）
A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{5π}{6}$
4．记区间（x1，x2）的长度为L=x2-x1，已知函数$f（x）=\frac{1}{3}a{x^2}+\frac{1}{2}b{x^2}+cx+d$（a＞b＞c），其图象在点（1，f（1））处的切线斜率为0，则函数f（x）单调递减区间的长度L的取值范围为（　　）
A．$（{1，\frac{3}{2}}）$B．$（{\frac{3}{2}，3}）$C．（1，3）D．（2，3）
14．已知函数f（x）=x2-2x，g（x）=ax-1，若?x1∈[-1，2]，?x2∈[-1，2]，使得f（x1）=g（x2），求a的取值范围．
1．若关于x的方程|x3-ax2|=x有不同的四解，则a的取值范围为（　　）
A．a＞1B．a＜1C．a＞2D．a＜2
18．已知抛物线C：y2=2px（p＞0）的焦点坐标为F（$\frac{1}{2}$，0）．
（Ⅰ）求p的值；
（Ⅱ）已知斜率为2的直线l与抛物线C相交于与原点不重合的两点A，B，且OA⊥OB，求l的方程．
19．（Ⅰ）计算：cos（-$\frac{19π}{6}$）；
（Ⅱ）已知x∈[$\frac{π}{2}$，$\frac{3π}{2}$]，且sinx=-$\frac{3}{5}$，求tanx的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网