题目内容
14.已知直线l经过两条直线2x+3y-14=0和x+2y-8=0的交点,且与直线2x-2y-5=0平行.(Ⅰ) 求直线l的方程;
(Ⅱ) 求点P(2,2)到直线l的距离.
分析 (Ⅰ) 求出交点坐标,求出斜率即可求直线l的方程;
(Ⅱ) 利用点到直线的距离公式之间求解点P(2,2)到直线l的距离.
解答 解:(Ⅰ)联立$\left\{\begin{array}{l}2x+3y-14=0\\ x+2y-8=0\end{array}\right.$,解得其交点坐标为(4,2).…(2分)
因为直线l与直线2x-2y-5=0平行,所以直线l的斜率为1.…(4分)
所以直线l的方程为y-2=1×(x-4),即x-y-2=0.…(6分)
(Ⅱ) 点P(2,2)到直线l的距离为$d=\frac{{|{2-2-2}|}}{{\sqrt{{1^2}+{{({-1})}^2}}}}=\frac{2}{{\sqrt{2}}}=\sqrt{2}$.…(10分)
点评 本题考查直线方程的求法,点到直线距离公式的应用,考查计算能力.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
2.已知命题p:“若直线a与平面α内两条直线垂直,则直线a与平面α垂直”,命题q:“存在两个相交平面垂直于同一条直线”,则下列命题中的真命题为( )
| A. | p∧q | B. | p∨q | C. | ¬p∨q | D. | p∧¬q |
19.下列函数中,在其定义域内是偶函数为( )
| A. | $f(x)=\frac{1}{x}$ | B. | f(x)=2x | C. | f(x)=lgx | D. | f(x)=cosx |
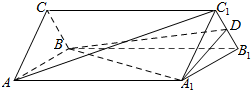 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.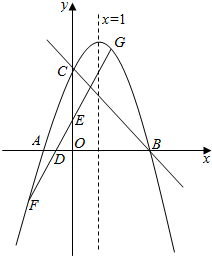 如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6.
如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6.