题目内容
利用公式求下列三角函数值.
(1)sin(-
π);
(2)cos(-
π).
(1)sin(-
| 7 |
| 6 |
(2)cos(-
| 79 |
| 6 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:直接利用诱导公式化简,得到特殊角的三角函数值即可.
解答:
解:(1)sin(-
π)=-sin(π+
)=sin
=
;
(2)cos(-
π)=cos
π=cos(12π+
)=cos(π+
)=-cos
=-
.
| 7 |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
(2)cos(-
| 79 |
| 6 |
| 79 |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
点评:本题考查诱导公式的应用,特殊角的三角函数值的求法,基本知识的考查.

练习册系列答案
相关题目
若直线a与平面α不垂直,那么平面α内与直线a垂直的直线有( )
| A、0条 | B、1条 |
| C、无数条 | D、不确定 |
如图所示是一个四棱锥的三视图,则该几何体的体积为( )
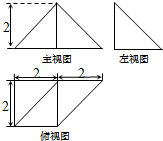

| A、4 | ||||
B、
| ||||
| C、12 | ||||
D、
|
 如图,C是以AB为直径的半圆O上的一点,过C的直线交直线AB于E,交过A点的切线于D,BC∥OD.若AD=AB=2,则EB=
如图,C是以AB为直径的半圆O上的一点,过C的直线交直线AB于E,交过A点的切线于D,BC∥OD.若AD=AB=2,则EB=