题目内容
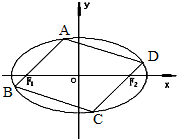 已知椭圆C:
已知椭圆C:| x2 |
| 4 |
| A、2 | ||
B、4
| ||
| C、4 | ||
| D、8 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:设椭圆C的内接平行四边形ABCD,写出直线AB、CD的方程,求出|AB|以及平行线AB、CD的距离d;
写出平行四边形ABCD的面积S的表达式,求出它的最大值.
写出平行四边形ABCD的面积S的表达式,求出它的最大值.
解答:
解:∵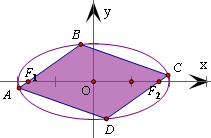 椭圆C:
椭圆C:
+y2=1,
∴焦点F1(-
,0),F2(
,0);
设椭圆C的内接平行四边形为四边形ABCD,如图所示
直线AB的方程为y=k(x+
),直线CD的方程为y=k(x-
),
则由
消去y,得(1+4k2)x2-8
k2x+4(3k2-1)=0;
设A(x1,y1),B(x2,y2),
∴x1+x2=
,x1x2=
;
∴|x1-x2|=
=
,
∴|AB|=
|x1-x2|=
;
由平行线间的距离公式,得直线AB、CD的距离d=
;
∴平行四边形ABCD的面积S=|AB|×d=8
•
;
令t=
=
=
+
,
再令
k2-
=s,显然当k2>
时,s>0,t=
+
>
,此时可取到最大值;
∴t=
+
=
+
≤
+
=
;
∴平行四边形ABCD的面积S=8
•
≤8
×
=4,
当且仅当k=±
时,平行四边形ABCD的面积S取得最大值4.
故选:C.
 椭圆C:
椭圆C:| x2 |
| 4 |
∴焦点F1(-
| 3 |
| 3 |
设椭圆C的内接平行四边形为四边形ABCD,如图所示
直线AB的方程为y=k(x+
| 3 |
| 3 |
则由
|
| 3 |
设A(x1,y1),B(x2,y2),
∴x1+x2=
8
| ||
| 1+4k2 |
| 4(3k2-1) |
| 1+4k2 |
∴|x1-x2|=
| (x1+x2)2-4x1x2 |
4
| ||
| 1+4k2 |
∴|AB|=
| 1+k2 |
| 4(1+k2) |
| 1+4k2 |
由平行线间的距离公式,得直线AB、CD的距离d=
2
| ||
|
∴平行四边形ABCD的面积S=|AB|×d=8
| 3 |
|
令t=
| k2(1+k2) |
| (1+4k2)2 |
(
| ||||||
| (1+4k2)2 |
| 1 |
| 16 |
| ||||
| (1+4k2)2 |
再令
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 8 |
| 1 |
| 16 |
| ||||
| (1+4k2)2 |
| 1 |
| 16 |
∴t=
| 1 |
| 16 |
| s | ||
64s2+24s+
|
| 1 |
| 16 |
| 1 | ||
24+(64s+
|
| 1 |
| 16 |
| 1 | ||||
24+
|
| 1 |
| 12 |
∴平行四边形ABCD的面积S=8
| 3 |
| t |
| 3 |
|
当且仅当k=±
| ||
| 2 |
故选:C.
点评:本题考查了求椭圆的内接平行四边形的面积问题,也考查了椭圆的简单几何性质、直线与圆锥曲线的位置关系以及基本不等式的应用问题,是综合题.

练习册系列答案
相关题目
实数a,b均为正数,且a+b=2,则
+
的最小值为( )
| 1 |
| a |
| 2 |
| b |
| A、3 | ||||
B、3+2
| ||||
| C、4 | ||||
D、
|
在△ABC中,内角A,B,C的对边分别为a,b,c,若a=18,b=24,A=45°,则这样的三角形有( )
| A、0个 | B、两个 |
| C、一个 | D、至多一个 |
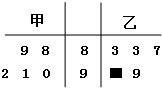 如图所示的茎叶图表示的是甲、乙两人在五次综合测评中的成绩,期中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为( )
如图所示的茎叶图表示的是甲、乙两人在五次综合测评中的成绩,期中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
设A,B,C为圆O上三点,且AB=3,AC=5,则
•
=( )
| AO |
| BC |
| A、-8 | B、-1 | C、1 | D、8 |
下列函数中值域为(0,+∞)的是( )
A、y=
| ||||
B、y=(
| ||||
C、y=
| ||||
D、y=
|
已知数列a1=2中,a1=2,an+1=an+
(n∈N*),则a101的值( )
| 1 |
| 2 |
| A、50 | B、51 | C、52 | D、53 |
已知α为锐角,且sin(α-
)=
,则sinα=( )
| π |
| 4 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|