题目内容
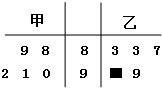 如图所示的茎叶图表示的是甲、乙两人在五次综合测评中的成绩,期中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为( )
如图所示的茎叶图表示的是甲、乙两人在五次综合测评中的成绩,期中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:茎叶图
专题:概率与统计
分析:根据茎叶图计算甲乙的平均数,利用古典概率的概率公式即可得到结论.
解答:
解:由茎叶图知:
=
(88+89+90+91+92)=90,
设被污损的数字为a,
=
(83+83+87+90+99+a)=88.4+
,
∵甲的平均成绩不超过乙的平均成绩,
∴88.4+
≥90,解得a≥8,∴a=8或a=9,
∴甲的平均成绩不超过乙的平均成绩的概率为
=
,
故选:D.
. |
| x甲 |
| 1 |
| 5 |
设被污损的数字为a,
. |
| x乙 |
| 1 |
| 5 |
| a |
| 5 |
∵甲的平均成绩不超过乙的平均成绩,
∴88.4+
| a |
| 5 |
∴甲的平均成绩不超过乙的平均成绩的概率为
| 2 |
| 10 |
| 1 |
| 5 |
故选:D.
点评:本题主要考查古典概率的计算,利用茎叶图求出x的值是解决本题的关键.

练习册系列答案
相关题目
下列转化结果错误的是( )
A、67°30'化成弧度是
| ||
B、-
| ||
C、
| ||
D、-150°化成弧度是
|
 如图,已知正方形ABCD是圆M:(x-4)2+(y-4)2=4的内接正方形,AB,AD的中点分别是E,F,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时则
如图,已知正方形ABCD是圆M:(x-4)2+(y-4)2=4的内接正方形,AB,AD的中点分别是E,F,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时则| ME |
| OF |
A、[-8
| ||||
| B、[-8,8] | ||||
C、[-4
| ||||
| D、[-4,4] |
如图是由一些火柴棒拼成的一系列图形,如第1个图中有4根火柴棒,第2个图中有7根火柴棒,则在第51个图中有火柴棒( )


| A、150根 | B、153根 |
| C、154根 | D、156根 |
已知等差数列{an}的首项为a,公差为d,且方程ax2-3x+2=0的解为1和d,则数列{3n-1an}的前n项和Tn为( )
| A、3n |
| B、1+(n-1)3n |
| C、n•3n |
| D、1+(n+1)•3n |
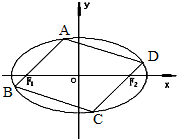 已知椭圆C:
已知椭圆C: