题目内容
某圆的圆心在直线y=2x上,并且在两坐标轴上截得的弦长分别为4和8,则该圆的方程为 .
考点:圆的标准方程
专题:直线与圆
分析:由已知设圆心为(a,2a),半径为R,则R2=a2+4=4a2+16或R2=a2+16=4a2+4,由此能求出圆的方程.
解答:
解:由已知设圆心为(a,2a),半径为R,
则R2=a2+4=4a2+16或R2=a2+16=4a2+4,
解得a=±2,
∴该圆的方程为(x-2)2+(y-4)2=20或(x+2)2+(y+4)2=20.
故答案为:(x-2)2+(y-4)2=20或(x+2)2+(y+4)2=20.
则R2=a2+4=4a2+16或R2=a2+16=4a2+4,
解得a=±2,
∴该圆的方程为(x-2)2+(y-4)2=20或(x+2)2+(y+4)2=20.
故答案为:(x-2)2+(y-4)2=20或(x+2)2+(y+4)2=20.
点评:本题考查圆的方程的求法,是基础题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
相关题目
等差数列{an}的前n项和为Sn,a12,a14是x2-x-2=0的两个根,则S25等于( )
A、
| ||
| B、5 | ||
C、-
| ||
| D、-5 |
设f(x)=
,则f(f(
))=( )
|
| 10 |
| A、e | B、1 | C、2 | D、以上都不对 |
设集合S={x|x2-2x=0x∈R},T={x|x2+2x-3≤0,x∈R},则S∩T=( )
| A、{0,2} |
| B、{0} |
| C、{0,-2} |
| D、{2,0,-2} |
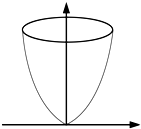 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是