题目内容
已知cos（π+α）=
，则cos（3π-α）的值是（ ）
| 4 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：已知等式左边利用诱导公式化简求出cosα的值，原式利用诱导公式化简后将cosα的值代入计算即可求出值．
解答：
解：∵cos（π+α）=-cosα=
，即cosα=-
，
∴cos（3π-α）=cos（π-α）=-cosα=
．
故选：A．
| 4 |
| 5 |
| 4 |
| 5 |
∴cos（3π-α）=cos（π-α）=-cosα=
| 4 |
| 5 |
故选：A．
点评：此题考查了运用诱导公式化简求值，以及同角三角函数基本关系的运用，熟练掌握诱导公式是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数f（x）在定义域R内可导，若对x∈R，恒有f（1+x）=f（1-x），且当x∈（-∞，1）时，（x-1）f′（x）＜0，设a=f（0），b=f（
），c=f（3），则（ ）
| 1 |
| 2 |
| A、b＜c＜a |
| B、c＜a＜b |
| C、c＜b＜a |
| D、a＜b＜c |
阅读如图的程序框图，若输出的S的值为30，则在判断框中应填入（ ）
| A、i＞3？ | B、i＞4？ |
| C、i＞5？ | D、i＜4？ |
f（x）=2x+3x的一个零点所在的一个区间是 （ ）
| A、（1，2） |
| B、（0，1） |
| C、（-1，0） |
| D、（-2，-1） |
在长方体ABCD-A1B1C1D1中，∠AB1B=45°，∠CB1C1=60°，则异面直线AB1与A1D所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
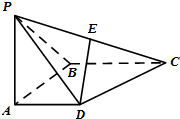如图，在四棱锥P-ABCD中，侧面PAB⊥底面ABCD，且∠PAB=∠ABC=90°，AD∥BC，PA=AB=BC=2AD，E是PC的中点．