题目内容
7.已知函数f(x)是定义在R上的偶函数,若方程f(x+1)=|x2+2x-3|的实根分别为x1,x2,…,xn,则x1+x2+…+xn=( )| A. | n | B. | -n | C. | -2n | D. | -3n |
分析 由题意,f(x+1)=|x2+2x-3|的对称轴为x=-1,方程f(x+1)=|x2+2x-3|的实根分别为x1,x2,…,xn,一个零点x1关于对称轴的对称点是x2,满足x1+x2=-2,即可得出结论.
解答 解:由题意,n是偶数,y=f(x+1),y=|x2+2x-3|的对称轴均为x=-1,
∵方程f(x+1)=|x2+2x-3|的实根分别为x1,x2,…,xn,
∴一个实根x1关于对称轴的对称点是x2,满足x1+x2=-2,
∴x1+x2+…+xn=-2•$\frac{n}{2}$=-n.
当n为奇数时,x=-1为一个实根,同样有x1+x2+…+xn=-1+(-2)•$\frac{n-1}{2}$=-n.
故选B.
点评 本题考查函数的奇偶性,函数的零点,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
17.已知$sinx+cosx=\frac{{\sqrt{3}-1}}{2}$,x∈(0,π),则tanx=( )
| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
18.已知幂函数f(x)=xα的图象过点$(2,\frac{1}{2})$,则函数g(x)=(x-2)f(x)在区间$[{\frac{1}{2},1}]$上的最小值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
2.在公差d=3的等差数列{an}中,a2+a4=-2,则数列{|an|}的前10项和为( )
| A. | 127 | B. | 125 | C. | 89 | D. | 70 |
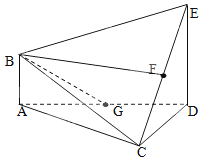 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点,F是CE的中点.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点,F是CE的中点.