题目内容
17.已知$sinx+cosx=\frac{{\sqrt{3}-1}}{2}$,x∈(0,π),则tanx=( )| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
分析 先根据sinx+cosx的值和二者的平方关系联立求得sinx、cosx的值,进而利用商数关系求得tanx的值.
解答 解:∵$sinx+cosx=\frac{{\sqrt{3}-1}}{2}$,x∈(0,π),
∴两边平方得2sinxcosx=-$\frac{\sqrt{3}}{2}$,cosx<0
∴(sinx-cosx)2=1-2sinxcosx=$\frac{\sqrt{3}+2}{2}$,
∵sinx-cosx>0,
∴sinx-cosx=$\frac{\sqrt{3}+1}{2}$,
与$sinx+cosx=\frac{{\sqrt{3}-1}}{2}$,联立
解得sinx=$\frac{\sqrt{3}}{2}$,cosx=-$\frac{1}{2}$,
∴tanx=$\frac{sinx}{cosx}$=-$\sqrt{3}$.
故选:D.
点评 本题主要考查了同角三角函数的基本关系的应用.解题的过程中要特别注意根据角的范围确定三角函数值的正负号.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知命题$p:x≠\frac{π}{6}+2kπ,k∈Z$;命题$q:sinx≠\frac{1}{2}$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
若y关于t的线性回归方程为$\stackrel{∧}{y}$=0.5t+a,则据此该地区2017年农村居民家庭人均纯收入约为( )
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
| A. | 6.3千元 | B. | 7.5千元 | C. | 6.7千元 | D. | 7.8千元 |
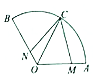 如图,扇形AOB所在圆的半径是1,弧AB的中点为C,动点M,N分别在OA,OB上运动,且满足OM=BN,∠AOB=120°.
如图,扇形AOB所在圆的半径是1,弧AB的中点为C,动点M,N分别在OA,OB上运动,且满足OM=BN,∠AOB=120°.