题目内容
已知函数f(x)=x2,x∈[-1,1],则函数y=f(2-x)的值域是 .
考点:函数的值域,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:先求出函数y=f(2-x)的解析式,然后求出自变量x的范围,根据二次函数的单调性求函数y的值域.
解答:
解:由x∈[-1,1]得-1≤2-x≤1,解得1≤x≤3;
y=f(2-x)=(2-x)2=(x-2)2;
∴函数y=f(2-x)在x=2取得最小值0,又x=1,时y=1;x=3时,y=1;
∴0≤f(2-x)≤1;
∴函数y=f(2-x)的值域是[0,1].
故答案为:[0,1].
y=f(2-x)=(2-x)2=(x-2)2;
∴函数y=f(2-x)在x=2取得最小值0,又x=1,时y=1;x=3时,y=1;
∴0≤f(2-x)≤1;
∴函数y=f(2-x)的值域是[0,1].
故答案为:[0,1].
点评:需要注意的是,需要求出函数y的自变量x的取值范围,并掌握求x取值范围的方法,就是由x∈[-1,1],得到-1≤2-x≤1,解这个不等式便是所要求x的取值范围.再一个需要对二次函数的单调性熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正方体A1B1C1D1-ABCD中,AB与B1D1成的角是( )
| A、30° | B、45° |
| C、60° | D、90° |
若α是第二象限角,sin
=
,则sinα=( )
| α |
| 2 |
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
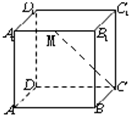 如图,在正方体ABCD-A1B1C1D1中,M为A1B1的中点,则MC与平面ABCD所成角的正弦值等于( )
如图,在正方体ABCD-A1B1C1D1中,M为A1B1的中点,则MC与平面ABCD所成角的正弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
总周长为12m的钢条制作一个长方体容器的框架,如果所制作容器的底面的相邻两边长之比为1:2,那么容器容积最大时,长方体的高为( )
| A、2m | B、1m |
| C、1.6m | D、3m |
 如图,在平面直角坐标系xOy中,钝角α的终边与单位圆交于B点,且点B的纵坐标为
如图,在平面直角坐标系xOy中,钝角α的终边与单位圆交于B点,且点B的纵坐标为