题目内容
设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x+2014)2f(x+2014)-4f(-2)<0的解集为( )
| A、(-∞,-2012) |
| B、(-2012,0) |
| C、(-∞,-2016) |
| D、(-2016,-2014) |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:通过观察2f(x)+xf′(x)>x2,不等式的左边像一个函数的导数,又直接写不出来,对该不等式两边同乘以x,∵x<0,∴会得到2xf(x)+x2f′(x)<x3,而这时不等式的左边是(x2f(x))′,所以构造函数F(x)=x2f(x),则能判断该函数在(-∞,0)上是减函数.这时F(x+2014)=(x+2014)2f(x+2014),F(-2)=4f(-2),而到这会发现不等式(x+2014)2f(x+2014)-4f(-2)<0可以变成F(x+2014)<F(-2),从而解这个不等式便可,而这个不等式利用F(x)的单调性可以求解.
解答:
解:由2f(x)+xf′(x)>x2,(x<0);
得:2xf(x)+x2f′(x)<x3
即[x2f(x)]′<x3<0;
令F(x)=x2f(x);
则当x<0时,F'(x)<0,即F(x)在(-∞,0)上是减函数;
∴F(x+2014)=(x+2014)2f(x+2014),F(-2)=4f(-2);
即不等式等价为F(x+2014)-F(-2)<0;
∵F(x)在(-∞,0)是减函数;
∴由F(x+2014)<F(-2)得,x+2014>-2,∴x>-2016;
又x+2014<0,∴x<-2014;
∴-2016<x<-2014.
∴原不等式的解集是(-2016,-2014).
故答案选D.
得:2xf(x)+x2f′(x)<x3
即[x2f(x)]′<x3<0;
令F(x)=x2f(x);
则当x<0时,F'(x)<0,即F(x)在(-∞,0)上是减函数;
∴F(x+2014)=(x+2014)2f(x+2014),F(-2)=4f(-2);
即不等式等价为F(x+2014)-F(-2)<0;
∵F(x)在(-∞,0)是减函数;
∴由F(x+2014)<F(-2)得,x+2014>-2,∴x>-2016;
又x+2014<0,∴x<-2014;
∴-2016<x<-2014.
∴原不等式的解集是(-2016,-2014).
故答案选D.
点评:本题考查函数的单调性与导数的关系,两个函数乘积的导数的求法,而构造函数是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若α是第二象限角,sin
=
,则sinα=( )
| α |
| 2 |
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
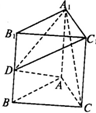 如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为( )
如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
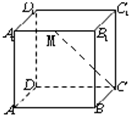 如图,在正方体ABCD-A1B1C1D1中,M为A1B1的中点,则MC与平面ABCD所成角的正弦值等于( )
如图,在正方体ABCD-A1B1C1D1中,M为A1B1的中点,则MC与平面ABCD所成角的正弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
观察下列各式:
=2
,
=3
,
=4
,….若
=9
,则n-m=( )
2-
|
|
3-
|
|
4-
|
|
9-
|
|
| A、43 | B、57 | C、73 | D、91 |
甲同学参加一次英语口语考试,已知在备选的10道题中,甲能答对其中的5道题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2道题才算合格.则甲合格的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
等差数列{an}中,若a7-a3=20,则a2014-a2008=( )
| A、40 | B、30 | C、25 | D、20 |