题目内容
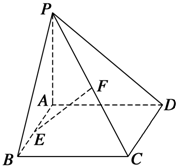 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.求证:
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.求证:(1)CD⊥PD;
(2)EF⊥平面PCD.
考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由线面垂直得CD⊥PA,由矩形性质得CD⊥AD,由此能证明CD⊥PD.
(2)取PD的中点G,连结AG,FG.由已知条件推导出四边形AEFG是平行四边形,所以AG∥EF.再由已知条件推导出EF⊥CD,由此能证明EF⊥平面PCD.
(2)取PD的中点G,连结AG,FG.由已知条件推导出四边形AEFG是平行四边形,所以AG∥EF.再由已知条件推导出EF⊥CD,由此能证明EF⊥平面PCD.
解答:
 (本题满分8分)
(本题满分8分)
证明:(1)∵PA⊥底面ABCD,∴CD⊥PA.
又矩形ABCD中,CD⊥AD,且AD∩PA=A,
∴CD⊥平面PAD,∴CD⊥PD.(4分)
(2)取PD的中点G,连结AG,FG.
又∵G、F分别是PD、PC的中点,
∴GF平行且等于
CD,
∴GF平行且等于AE,
∴四边形AEFG是平行四边形,∴AG∥EF.
∵PA=AD,G是PD的中点,
∴AG⊥PD,∴EF⊥PD,
∵CD⊥平面PAD,AG?平面PAD.
∴CD⊥AG.∴EF⊥CD.
∵PD∩CD=D,∴EF⊥平面PCD.(8分)
 (本题满分8分)
(本题满分8分)证明:(1)∵PA⊥底面ABCD,∴CD⊥PA.
又矩形ABCD中,CD⊥AD,且AD∩PA=A,
∴CD⊥平面PAD,∴CD⊥PD.(4分)
(2)取PD的中点G,连结AG,FG.
又∵G、F分别是PD、PC的中点,
∴GF平行且等于
| 1 |
| 2 |
∴GF平行且等于AE,
∴四边形AEFG是平行四边形,∴AG∥EF.
∵PA=AD,G是PD的中点,
∴AG⊥PD,∴EF⊥PD,
∵CD⊥平面PAD,AG?平面PAD.
∴CD⊥AG.∴EF⊥CD.
∵PD∩CD=D,∴EF⊥平面PCD.(8分)
点评:本题考查异面直线垂直的证明,考查直线垂直于平面的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
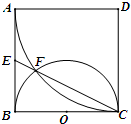 如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.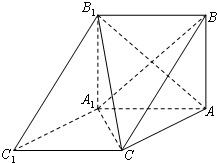 如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2
如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.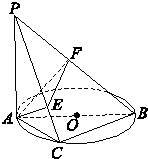 如图所示,已知PA⊥⊙O所在平面,AB是⊙O的直径,点C是⊙O上任意一点,过A作AE⊥PC于点E,AF⊥PB于点F,求证:
如图所示,已知PA⊥⊙O所在平面,AB是⊙O的直径,点C是⊙O上任意一点,过A作AE⊥PC于点E,AF⊥PB于点F,求证: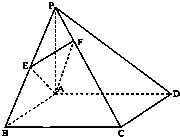 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,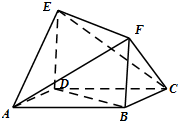 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,