题目内容

12．下列函数中，在区间（0，+∞）上为增函数的是（　　）
A．y=-log2xB．$y=-\frac{1}{{\sqrt{x+1}}}$C．$y={（\frac{1}{2}）^x}$D．$y=2x+\frac{1}{x}$

分析 根据函数单调性的性质进行判断即可．

解答 解：y=-log2x在区间（0，+∞）上为减函数，不满足条件．
$y=-\frac{1}{{\sqrt{x+1}}}$在区间（0，+∞）上为增函数，满足条件．
$y={（\frac{1}{2}）^x}$在区间（0，+∞）上为减函数，不满足条件．
$y=2x+\frac{1}{x}$的导数f′（x）=2-$\frac{1}{{x}^{2}}$=$\frac{2{x}^{2}-1}{{x}^{2}}$
由f′（x）=0得x=$\frac{\sqrt{2}}{2}$，
则当x＞$\frac{\sqrt{2}}{2}$时，f′（x）＞0，此时函数单调递增，
当0＜x＜$\frac{\sqrt{2}}{2}$时，f′（x）＜0，此时函数单调递减，
即函数在区间（0，+∞）上不是增函数，不满足条件．
故选：B

点评 本题主要考查函数单调性的判断，根据函数的性质以及利用导数研究函数的单调性是解决本题的关键．

练习册系列答案
相关题目
4．某公司生产某种产品的固定成本为150万元，而每件产品的可变成本为2500元，每件产品的售价为3500元．若该公司所生产的产品全部销售出去．则：
（1）分别求出总成本y1（单位：万元），单位成本y2（单位：万元），销售总收人y3（单位：万元），总利润y4（单位：万元）与总产量x（单位：件）的函数解析式；
（2）根据所求函数的图象，对这个公司的经济效益作出简单分析．
3．给出下列四个命题：
①若f′（x0）=0，则函数y=f（x）在x=x0取得极值；
②若m≥-1，则函数y=log${\;}_{\frac{1}{2}}$（x2-2x-m）的值域为R；
③“函数f（x）=$\frac{a-{e}^{x}}{1+a{e}^{x}}$在定义域内是奇函数”的充分不必要条件是“a=1”；
④定义在R上的函数y=f（x）满足条件f（x+$\frac{3}{2}$）=-f（x），且y=f（x-$\frac{3}{4}$）为奇函数，则f（x）为R上的偶函数．
其中正确的命题序号是②③④．
20．下列各组中的两个函数是相等函数的是（　　）
A．y=x与y=$\frac{{x}^{2}}{x}$B．y=（$\sqrt{x}$）2-1与y=|x|-1C．y=x2与y=$\root{3}{{x}^{6}}$D．y=$\root{3}{{x}^{3}}与y=\sqrt{{x}^{2}}$
7．过点A（1，-2）且斜率为3的直线方程是（　　）
A．3x-y+1=0B．3x+y-5=0C．3x-y-5=0D．3x+y-1=0
17．正方体ABCD-A1B1C1D1中，E，F，G分别在棱AB，CC1，D1A1上，且正方体的棱长为a，AE=CF=D1G=b，则DB1与平面EFG所成角为（　　）
A．75°B．60°C．90°D．15°
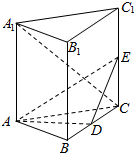4．已知三棱柱ABC-A1B1C1，侧棱AA1垂直于底面ABC，∠ABC=$\frac{π}{2}$，AB=BC=AA1=4，D为BC的中点．
（1）若E为棱CC1的中点，求证：DE⊥A1C；
（2）若E为棱CC1上异于端点的任意一点，设CE与平面ADE所成角为α，求满足sinα=$\frac{4\sqrt{61}}{61}$时CE的长．
1．如图，有一块矩形空地，要在这块空地上开辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB=a（a＞2），BC=2，且AE=AH=CF=CG，设AE=x，绿地面积为y．
（1）写出y关于x的函数关系式，并指出这个函数的定义域；
（2）当AE为何值时，绿地面积y最大？
2．设a=20.2，b=ln2，c=log2$\frac{9}{10}$，则a，b，c的大小关系是（　　）
A．a＞b＞cB．a＞c＞bC．b＞a＞cD．b＞c＞a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网