题目内容
函数y=ln(x+1)与y=
的图象交点的横坐标所在区间为( )
| 1 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
考点:函数零点的判定定理
专题:转化思想,函数的性质及应用
分析:该问题可转化为方程ln(x+1)=
的解的问题,进一步可转化为函数f(x)=ln(x+1)-
的零点问题.
| 1 |
| x |
| 1 |
| x |
解答:
解:令f(x)=ln(x+1)-
,
∵f(2)=ln3-
>1-
>0,f(1)=ln2-1<lne-1=0,
又函数f(x)在(1,2)上的图象是一条连续不断的曲线,
∴函数f(x)在区间(1,2)内有零点,即ln(x+1)=
有解,
此解即为函数y=ln(x+1)与y=
的图象交点的横坐标.
故选:B.
| 1 |
| x |
∵f(2)=ln3-
| 1 |
| 2 |
| 1 |
| 2 |
又函数f(x)在(1,2)上的图象是一条连续不断的曲线,
∴函数f(x)在区间(1,2)内有零点,即ln(x+1)=
| 1 |
| x |
此解即为函数y=ln(x+1)与y=
| 1 |
| x |
故选:B.
点评:本题考查函数零点的存在问题,本题中函数y=ln(x+1)与y=
的图象交点的横坐标,可转化为函数f(x)=ln(x+1)-
的零点.注意函数与方程思想、转化与化归思想的运用.
| 1 |
| x |
| 1 |
| x |

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2]时,f(x)=
,若x∈[-2,0]时,f(x)≥
-
恒成立,则实数t的取值范围是( )
|
| t |
| 2 |
| 1 |
| t |
| A、[-2,0)∪(0,1) |
| B、[-2,0)∪[1,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪(0,1] |
阅读如图所示的程序框图,则该算法的功能是( )
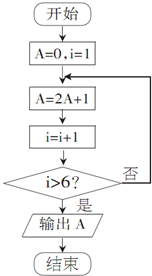

| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前6项的和 |
| C、计算数列{2n-1}前5项的和 |
| D、计算数列{2n-1}前6项的和 |
已知A,B,C是单位圆O上任意的不同三点,若
=2
+x
,则正实数x的取值范围为( )
| OA |
| OB |
| OC |
| A、(0,2] |
| B、[1,3] |
| C、[2,4] |
| D、[3,5] |
已知在一个120°的二面角的棱上有两个点A、B,AC、BD分别是在这个二面角的两个半平面内且垂直于AB的线段,又AB=4cm,AC=6cm,BD=8cm,则CD的长为( )
A、2
| ||
B、
| ||
C、2
| ||
D、4
|

 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.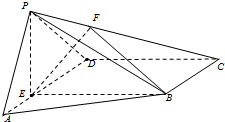 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.