题目内容
如图,已知f(x)=ax3+bx2+cx+d(a≠0),记△=4b2-12ac则当△>0且a>0时,f(x)的 大致图象为( )
A、 |
B、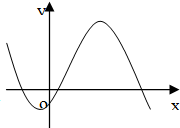 |
C、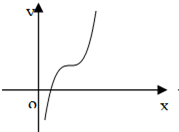 |
D、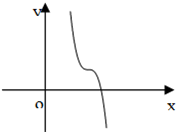 |
考点:函数的图象
专题:函数的性质及应用
分析:求出f(x)的导函数,三次函数的导数为二次函数,再利用二次函数的判别式与二次函数的零点的关系解题.
解答:
解:∵f(x)=ax3+bx2+cx+d(a≠0),
∴f′(x)=3ax2+2bx+c
∵a≠0),
∴f′(x)=3ax2+2bx+c为二次函数,
∵△=4b2-12ac>0
又∵a>0
∴f′(x)=0有两个不等的实数根,
故f(x)=ax3+bx2+cx+d在R上有两个极值点,∴AB符合,
∵x无限增大时,由于a为正数,函数值无限增大,只有A符合,
故选:A
∴f′(x)=3ax2+2bx+c
∵a≠0),
∴f′(x)=3ax2+2bx+c为二次函数,
∵△=4b2-12ac>0
又∵a>0
∴f′(x)=0有两个不等的实数根,
故f(x)=ax3+bx2+cx+d在R上有两个极值点,∴AB符合,
∵x无限增大时,由于a为正数,函数值无限增大,只有A符合,
故选:A
点评:本题考查二次函数的图象与判别式的关系、考查利用导函数研究原函数的极值.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知a<b<0,c<0,则下列各式正确的是( )
| A、ac<bc | ||||
B、
| ||||
| C、(a-2)c<(b-2)c | ||||
| D、a+c<b+c |
圆心在直线y=x上且与x轴相切于点(1,0)的圆的方程为( )
| A、(x-1)2+y2=1 |
| B、(x-1)2+(y-1)2=1 |
| C、(x+1)2+(y-1)2=1 |
| D、(x+1)2+(y+1)2=1 |
已知等差数列{an}的前n项和为Sn,a1=-12,|a8|=|a17|,则当Sn取最小值时,n等于( )
| A、12 | B、13 |
| C、11或12 | D、12或13 |
设α∈(0,π)若sinα+cosα=
,则cosα=( )
| 17 |
| 25 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知集合U={-1,0,1,2,3},P={-1,2,3},则∁UP=( )
| A、{0,1} |
| B、{-1,0,1} |
| C、{0,1,2} |
| D、{-1,0,1,2} |



